3. Основи ВС і AD трапеції ABCD дорівнюють вiдповiдно 10 см i 20 см. Відомо, що BAD=30º, CDA =60°. Знайдіть сторону CD.

CD=5см

Объяснение:

Опустим высоты ВЕ и CF из вершин B и C на основу AD. BE⟂AD, CF⟂AD. BE=CF=h.

EBCF - прямоугольник, поэтому EF=BC=10 см.

Следовательно AE+FD=AD-BC=20-10=10см

Пусть FD=x, тогда AE =10-x.

1) △ABE(∠E=90°)

h=BE=AE•tg 30°=(10-x)•(√3/3)

2)△CDF(∠F=90°)

h=FC=x•tg 60° = √3•x

BE=FC

Обе части равенства умножим на :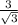

10-х=3х

4х=10

х=5/2

FD=5/2

CD=2•FD=2•(5/2)=5см

5

Объяснение:

Так как острые углы трапеци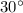и  и 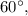продлим ее боковые стороны до пересечения в точке 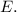Тогда образовавшийся треугольник 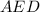прямоугольный.

Его катет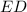 лежит напротив угла 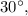а значит равен половине гипотенузы:

Треугольник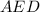и и 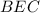подобны с коэффициентом

значит и боковая сторона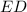 делится в том же отношении. То есть