"Логарифмические неравенства очень
Другие вопросы по теме Русский язык
Популярные вопросы
- Решить 3 класса. рыбак утром выехал из города на . расстояние от города до...
2 - Одного города. салтыков- щадриню тема романа ,главные герои , идея...
3 - Определите виды связи, чем образованы? so2, o2, nh3, cacl2, n2, al2o3, cus...
3 - 1. if they (play) better, they (win) the game. 2. if she (read) more carefully,...
3 - Животное: дельфин 1.определить среду обитания 2.выявить черты при выявить...
1 - Найдите наибольшее целое число, входящее в область допустимых значений выражения...
1 - Прочитай. определи время глаголов. запиши эти глаголы во множественном числе.выдели...
2 - С: для учеников начальных классов в школьной библиотеке есть 273учебника по...
2 - Нужен краткий рассказ о интернете(не как и где его изобрели)...
3 - Вопросы по великая отечественная война 1) меры которые проводились советским...
1
1)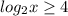
ОДЗ: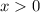
Так как основание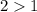 , то справедливо неравенство:
, то справедливо неравенство:
С учетом ОДЗ получаем решение:
ответ: (16; +∞)
2)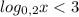
ОДЗ: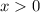
Так как основание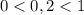 , то справедливо неравенство:
, то справедливо неравенство:
С учетом ОДЗ получаем решение:
ответ: (0,008; +∞)
3)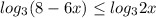
ОДЗ: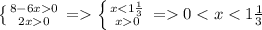
Так как основание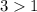 , то справедливо неравенство:
, то справедливо неравенство:
С учетом ОДЗ получаем решение:
ответ: [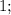
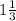 )
)