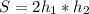Знайти площу паралелограма якщо. дві висоти паралелограма h1 і h2 а периметр у 4 рази більше за суму цих висот
Другие вопросы по теме Математика
Популярные вопросы
- радужная арка засверкала ярко,разукрасила траву,расцветила синеву . сколько...
3 - Вчемпричина сходствавсех животныхклеток?...
2 - Вычесли периметр прямоугольника со сторонами 4 см и 5см и начерти отрезок,...
3 - На идут 8 мальчиков: у четверых в руках удочки и у шестерых ведерки. есть...
1 - Опесать картину врублёва царевна лебедь...
1 - Квартира состоит из 3 комнат общей площадью 42 м2.первая комната по площади...
3 - :) укажите для каждого растения его основное в природе и в жизни человека:...
3 - Виноград содержит 90% влаги,а изюм 5.сколько килограммов винограда требуется...
1 - Запишите периодическую дробь в виде обыкновенной дроби: 8,7(21)...
3 - Вычислите сколько молекул и атомов содержит 1 моль кислорода...
1
Найти площадь параллелограмма если две высоты параллелограмма h₁ и h₂ а периметр в 4 раза больше суммы этих высот.
Дано:
Найти его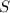
Решение.
Пусть одна сторона параллелограмма равна , тогда
, тогда
Находим его площадь:
Очевидно, что
Подставим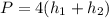 и решим уравнение относительно
и решим уравнение относительно  .
.
Находим его площадь:
ответ: