Завод выпускает партию электрических лампочек, состоящую
из 200000 штук. Вероятность того, что лампочка неисправна
составляет 0,0001. Найти вероятность того, что в партии 10 лампочек
бракованных.
2. Отклонение контролируемого размера от проектного подчинено нормальному закону распределения с параметрами а = 10 мм,
σ = 5 мм. Деталь считается годной, если отклонение ее размера от
контрольного не превышает 2,5 мм. Найти процент годных деталей,
которые изготовляет автомат. Указать допустимые границы отклонения контролируемого размера от а по модулю, которое можно
гарантировать с вероятностью 0,99.
Другие вопросы по теме Математика
Популярные вопросы
- К однородной нерастяжимой верёвке массой 50 г подвешен груз массой 400 г. Найдите...
2 - Tomorrow beaches day eaten fun got have like saw skins took Dear Carol, We really...
1 - 1. Визначте, хто з митців не був класиком соціально-психологічної прози: A)...
3 - Ha рисунке АС=20см иВА=ДС ВД цепь,формула цепа уравнение y=0,02x2+4,8 .точкиЕ,А,С,F...
2 - What is science???what is Biology??...
1 - В. Богомолов Иван для читательского дневника Основная мысль Моё мнение Тема...
1 - В фотошопе или в тетради в виде таблицы ПО ДРУГОМУ НЕ ПРИНЕМАЕТСЯ...
2 - Зависимость координаты от времени для некоторого тела описывается уравнением...
3 - Имеются 5 камней три одинаковых более легких и два одинаковых более тяжёлых...
1 - Знайти площу рівнобедреної трапеції, у якої довжини основ дорівнюють 10см і...
1
Відповідь:
Покрокове пояснення:
1) Собитие A ={ лампочка бракованная }
Р (А) =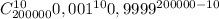
2) знайдемо ймовірність придатності деталі
Р (|Х - а | < 2, 5 ) = 2 Ф ( 25/2 ) = 0, 3850
Де Ф ( х ) функція Лапласса
Отже відсоток идатних деталей буде 38, 5
Щодо 0, 99 то це зворотня задача :
2Ф ( х ) = 0, 99. відповідає х = 1 , 56
Враховуючи. що сігма дорівнює 5 маємо, що з
ймовірністю 0, 99 деталь буде відхилятися не більше ніж на 7, 8