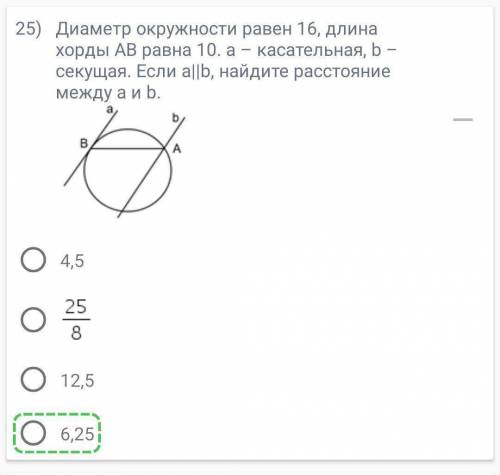
Задача про окружность (ответ отмечен,мне нужно решение)

Пошаговое объяснение:

Дано:

d = 16 см (диаметр окружности);

l AB l -10 см (длина секущей).

Найти:

Расстояние между прямыми а и в

Выполним дополнительные построения (см. рис. "касательная и секущая".

l ВС l = d - диаметр, Δ ABC - прямоугольный, прямой угол ∠А (как треугольник, опирающийся на диаметр).

Найдем величину l AC l (по теореме Пифагора):

l AC l=√(d²- l AB l²);

l AC l=√(16²-10²)=√(256-100)=√156=2√39;

Т.к. прямые а и в параллельны, то ∠ ADB - прямой. И, следовательно,

расстояние между касательной а и секущей в - l BD l равно диаметру окружности минус отрезок l DС l.

l BD l = d - l DС l

Обозначим длину отрезка  l DС l через х.

Рассмотрим поближе Δ ABC и Δ ADC (см рис. "подобные треугольники"). Эти треугольники прямоугольные, и, что самое важное, эти треугольники подобные (они имеют равные острые углы. ∠ACD = ∠ACB)!

А, как известно, у подобных треугольников стороны пропорциональны. Составим пропорцию (вспомнив, что против равных углов лежат пропорциональные стороны):

l AC l/x=d/l AC l;

x=l AC l²/d;

x=(2√39)²/16=(4*39)/16=39/4;

l BD l = d - l DС l ⇒ l BD l = d - x;

l BD l =16-39/4=64/4-39/4=25/4=6 1/4=6.25