Якщо від перших двох членів арифметичної прогресії відняти відповідно 5 і 4, а третій член щалишити без щмін, то отримаемо три перших члени геометричної прогресії. Знайти добуток цих трьох членів цієї арифметичнох прогресії, якщо їх сума дорівнює 30
Другие вопросы по теме Математика
Популярные вопросы
- Авто машина проехала 2 ч 30 мин со скоростью 35,2 км ч и 3 ч 20 мин...
1 - решите систему уравнений: {3x-2y=4, {2x+3y=7. в ответе должно получится...
3 - (х,75-1.4х)÷7-1,11 кто может решить...
1 - Составить 10 предложений по пяти пунктограммам срочьно...
1 - Подскажите , предложения с глаголом учёный....
2 - 2примера взаимодействие амфотерных оксидов с основными...
2 - You want to invite your english friend to your town for a few days.write...
2 - Почему на територий евразии природные зоны сменяются не только с севера...
1 - Что произойдет с землей если исчезнут ростения....
1 - Написать сочинение день защитника отечества. моей младшей сестре задали...
1
Если от первых двух членов арифметической прогрессии вычесть соответственно 5 и 4, а третий член третий член оставить без изменений, то получим три первых члена геометрической прогрессии. Найти произведение этих трех членов этой арифметической прогрессии, если их сумма равна 30.
Решение
1) По условию их сумма равна 30.
2) Согласно условию получим три члена геометрической прогрессии:
3)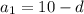
1) =>
=> 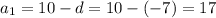
2)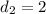 =>
=> 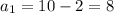
ответ: 510
960