Я не понимаю выражение ... 2(а+в)с+с²... и далее в выражении. Именно этот момент объясните подробно. И не дайте коротких лаконичных ответов. Иначе 1 звезда и жалоба.
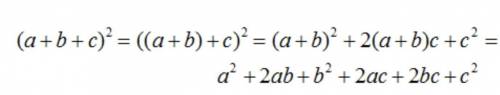
Другие вопросы по теме Математика
Популярные вопросы
- Вдвузначном числе переставили цифрвы и полученное число сложили...
3 - Установите соответствие между обозначением объекта на карте и...
2 - Во время весених каникул серёжа планировал решить 40 по за 5...
1 - На территории какого государства в северной америке находится...
2 - Как влияет среда обитания на строение свободно живущих и паразитических...
2 - Саша тренировал глазомер, оценивая длину некоторой дистанции...
2 - Дуже поясніть значення фразеологізмів.: курити фіміам - обдерти...
1 - Вкаком случае происходит вынужденная конвекция? а)согревание...
3 - На что был готов дубровский ради любви?...
2 - Докажи правильность выбора приставок дошёл до школы и пошёл к...
1
Пошаговое объяснение:
Чтобы понять этот момент, сначала надо разобраться с тем, что такое (x+y)^2
(x+y)^2=(x+y)(x+y)=x^2+xy+xy+y^2=x^2+2xy+y^2
Это довольно известная формула, проходится в школе и наверняка у тебя она была, это то, как раскрывается квадрат суммы двух слагаемых
Теперь, когда мы понимаем как раскрывается квадрат суммы двух слагаемых, можем ли мы понять как раскрывается квадрат суммы трех слагаемых?
То есть, еще раз, мы знаем что делать если слагаемых два (x+y)^2=x^2+2xy+y^2
А что делать если слагаемых три?
(a+b+c)^2=???
Можно попробовать применить хитрый ход и рассмотреть выражение a+b как одно слагаемое
Если это тяжело для понимания, то просто представь как будто ты сделала замену a+b=x; c=y
Тогда твое выражение (a+b+c)^2 превращается в (x+y)^2 и ты уже знаешь что с ним делать
У тебя (x+y)^2=x^2+2xy+y^2, после того как мы сделаем обратную замену (заменим x на a+b; y на c), получим следующую запись:
(a+b)^2+2(a+b)c+c^2
Пойдем дальше
(a+b)^2=a^2+2ab+b^2 (аналогично)
2(a+b)c=2ac+2bc
Итого
a^2+2ab+b^2+2ac+2bc+c^2, то что у них получилось в конце
Выражение 2(a+b)c+c^2 следует из Квадрата суммы. Например: (a+b) ^2=a^2+2ab+b^2;
Одно и то же для этого выражения:((a+b) +c) ^2=квадрату первого, то есть (a+b) ^2 + удвоенное произведение первого на второй, то есть 2(a+b)c + квадрат второго, то есть c^2. Надеюсь смог тебе объяснить. Если какие то вопросы возникнут можешь спросить!)))