1. Математика
  2. Y=7x^8-4cosx+7 выяснить обладает

Y=7x^8-4cosx+7 выяснить обладает ли функция четностью

Abl15 Abl15    3   01.11.2019 13:45    1

Ответы
DeRellik DeRellik  10.10.2020 10:39

ответ: Функция является чётной.

Пошаговое объяснение: Запишем уравнение в виде функции x.

f(x)=7x^8-4\cos (x)+7

Найдем f(-x).

Найдем f(-x), подставив -x везде вместо x в f(x).

f(-x)=7(-x)^8-4\cos (-(-x))+7

Упростим каждый член.

Применим правило произведения к -x.

f(-x)=7((-1)^8x^8)-4\cos(-(-x))+7

Возведем -1 в степень 8.

f(-x)=7(1x^8)-4\cos (-(-x))+7

Умножим x^8 на 1.

f(-x)=7x^8-4 \cos (-(-x))+7

Умножаем -(-x).

Умножим -1 на -1.

f(-x)=7x^8-4\cos (1x)+7

Умножим x на 1.

f(-x)=7x^8-4\cos (x)+7

Функция является чётной, если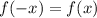 f(-x)=f(x).

Проверим, справедливо ли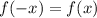 f(-x)=f(x).

7x^8-4\cos(x)+7=7x^8-4\cos (x)+7

Поскольку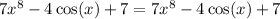 7x^8-4\cos(x)+7=7x^8-4\cos (x)+7, функция является чётной.

Функция является чётной.

ПОКАЗАТЬ ОТВЕТЫ
Aisuluuuuuuu Aisuluuuuuuu  10.10.2020 10:39

Пошаговое объяснение:Если ф-ция четная, то f(-x)=f(x)

y(-x)=7(-x)^8-4cos(-x)+7=7x^8-4cosx+7, значит ф-ция четная

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
smaliar2004 smaliar2004  13.08.2019 12:20
Преобразуйте обыкновенную дробь 5/9 в бесконечную периодическую десятичную дробь...
Pustynya Pustynya  13.08.2019 12:20
30 найдите неизвестное число и сделайте проверку подставив это число в уравнение 1) а+2546=3764 2) 46789-b =5788 3) c (умножить) 345=43815 4) 2898: d=23 5) x(делить)540=360...
anastasiya249 anastasiya249  13.08.2019 12:20
Как пот готовить для варкисупа рис , перловую крупу , фасоль ?...
igor2285 igor2285  13.08.2019 12:20
Выражения: 6a*7b 35x*23y 4a*9*b*c 2*(x+7) 7*(5-a) (c-8)*12 14(3a-2) 8(4a-3b+11c) (6x+4d-2z)*15 27c-c a+34a 12a+13a+26 59z-z+73 38x+17x-54x+x вот выражения и да x это...
Erkinbekulbosin Erkinbekulbosin  13.08.2019 12:20
На каком сайте можно найти олимпиады?...
sasuke97 sasuke97  13.08.2019 12:20
Является ли пара чисел (3; 1) решением уравнения? (надо решить, а не просто ответ написать) 5x(3 степень) -y=134 заранее...
Жибек20041 Жибек20041  13.08.2019 12:20
Один из углов при пересечении двух прямых равен 67°.найти остальнве угоы...
Feshiondiva Feshiondiva  13.08.2019 12:20
Основания трапеции относятся как 3: 7 , а средняя линия равна 77. найдите меньшее основание...
10672 10672  13.08.2019 12:20
Усаши втрое больше марок с роботами,чем у пети, а у пети на 6 таких марок меньше ,чем у саши. сколько таких марок у каждого? уравнением нельзя решать...
Licona Licona  13.08.2019 12:20
Тема прибор возможных вариантов запишите все трехзначные числа используя 0 8 9 только один раз сколько таких чисел получится решите с построение дерева...

Популярные вопросы