1. Математика
  2. Взятие частной производной. У

Взятие частной производной. У меня имеется следующее равенство:, где точка над переменной означает производную по t.
Также известно, что все 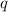q независимы. Тогда 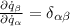\frac{\partial \dot q_{\beta}}{\partial \dot q_{\alpha}}=\delta_{\alpha \beta}, где дельта - это символ Кронекера.
Все это понятно, но непонятным становится следующий шаг.

Берут частную производную первого уравнения по 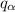q_{\alpha}:.
Почему мы получили символ Кронекера? Ведь должно было получиться что-то вроде этого:


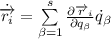
\dot{\overrightarrow{r_i}}=\sum\limits_{\beta=1}^s\frac{\partial \overrightarrow r_i}{\partial q_{\beta}}\dot q_{\beta}
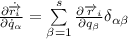
\frac{\partial \dot{\overrightarrow{r_i}}}{\partial \dot q_{\alpha}}=\sum\limits_{\beta=1}^s\frac{\partial \overrightarrow r_i}{\partial q_{\beta}}\delta_{\alpha \beta}
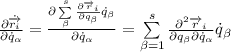
\frac{\partial \dot{\overrightarrow{r_i}}}{\partial \dot q_{\alpha}}=\frac{\partial \sum\limits_{\beta}^s\frac{\partial \overrightarrow r_i}{\partial q_{\beta}}\dot q_{\beta}}{\partial \dot q_{\alpha}}=\sum\limits_{\beta=1}^s \frac{\partial^2 \overrightarrow r_i}{\partial q_{\beta} \partial \dot q_{\alpha}}\dot q_{\beta}}

AMORVL AMORVL    1   25.01.2021 22:13    0

Ответы
Показать ответы (3)
Другие вопросы по теме Математика
Любчик908 Любчик908  03.12.2019 10:18
Висота циліндра втричі більша за його радіус а відрізок що сполучає центр верхньої основи з точкою кола нижньої основи дорівнює два корені з трьох знайдіть радіус і висоту...
kostyafadeev9 kostyafadeev9  03.12.2019 10:17
Вопрос не совсем школьного характера но все же напишу. 1373 км сколько по времени примерно? заранее ​...
Sasha2007ad Sasha2007ad  03.12.2019 10:16
Окружность делится двумя точками а и в на две части в отношении 7: 5. найти величины центральных углов, если оа и ов - радиусы​...
jonbraims jonbraims  03.12.2019 10:16
Правило зведення тригонометричних функцій до кутів 1 чверті...
gasimovaa44 gasimovaa44  03.12.2019 10:16
30 решить матричное уравнение...
Xmitejr Xmitejr  03.12.2019 10:15
Какие функции имеют период т=п...
Liza031111 Liza031111  03.12.2019 10:13
Вычислить интеграл (x^3-1/x^2-x)dx...
Whitecat111 Whitecat111  03.12.2019 10:09
Тема : функции нескольких переменных , : исследовать на экстремум следующую функцию z=x^2+y^2+xy-4x-5y...
f2a5p4 f2a5p4  03.12.2019 10:07
Площа осьового перерізу циліндру дорівнює 32 см2 знайдіть радіус і висоту циліндра якщо вони рівні...
ilacher12 ilacher12  03.12.2019 10:07
Дан треугольник abc. плоскость, параллельная прямой bc, пересекает сторону ab в точке b1, а сторону ac - в точке c1. найдите длину отрезка b1c1, если bc=6,3см, bb1: b1a=3:...

Популярные вопросы