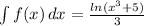ВЫСШАЯ МАТЕМАТИКА. Сравнение рядов!
На первой фотографии - интегральный признак, на второй - признак Коши. Я почти решила второй, но меня смущает последняя строка, где нужно написать степень числа "е". Я думаю, что е^(n-1), и при n, которая стремится к бесконечности, е получается в степени бесконечность=бесконечность и р. расход. Но это лишь мое предположение. Что касается первого - я пень ВЫСШАЯ МАТЕМАТИКА. Сравнение рядов! На первой фотографии - интегральный признак, на второй - призна">
Другие вопросы по теме Математика
Популярные вопросы
- Написать. алгоритм анализа системы : 1. форма правления, 2. органы законодательной...
1 - 1.was the museum (close) last month? a. close b. closed c. are closed d. is...
2 - Составьте формулы: 1) 2-хлор-1-фторпропан 2) 2,3 диэтилгексан 3) 2,3 дифторбутан...
2 - Сочинить небольшой стих или сочинение на тему школа...
2 - Напишіть невелику розповідь (6-8) речень з висловом ,,хто літом працює тойтв...
1 - Выполните действие а) √5*(4√75-√125)= б) √3*(√12-2√27)=...
1 - Знайти валентність елементів! 1.a)bah2,v2o5,sif4,li3p...
1 - А) what you for, dear? (to look) b) where you to spend your sunday (to go)...
1 - Сочинение на тему «гроза» 10 предложений...
3 - Собака, находясь в точке а, погналась за лисицей, которая была на расстоянии...
2
Пошаговое объяснение:
Смысл интегрального признака, в том,что при проверке сходимости ряда мы заменяем ряд на интеграл от выражения для ряда. В данном случае мы вычисляем интеграл для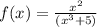 и смотрим,как он ведет себя на бесконечности. Если интеграл расходится, то будет расходится и ряд.
и смотрим,как он ведет себя на бесконечности. Если интеграл расходится, то будет расходится и ряд.