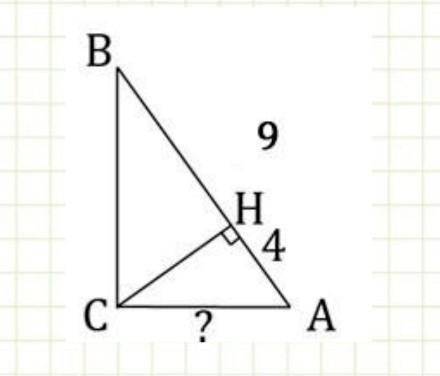
В треугольнике ABC угол C равен 90°, CH - высота, AB = 9, АH = 4. Найдите CА

по идее 7

Пошаговое объяснение:

но это не точно

Для решения данной задачи, нам понадобятся основные свойства треугольников и тригонометрические функции.Данное задание связано с прямым треугольником, в котором один из углов равен 90°.

1. Нам дано, что угол C равен 90°. Это означает, что треугольник ABC - прямоугольный треугольник.

2. Высотой в треугольнике называется отрезок, проведенный из вершины треугольника к основанию под прямым углом. В данном случае, CH является высотой, проведенной из вершины C.

3. Так как треугольник ABC - прямоугольный, то высота CH является перпендикуляром к гипотенузе AB. То есть, CH - это высота, опущенная из прямого угла C на гипотенузу AB.

4. Мы знаем, что AB = 9 и AH = 4. Поскольку CA является гипотенузой, данному значению будет соответствовать гипотенуза треугольника. Таким образом, применяя теорему Пифагора, мы можем найти CA:

CA^2 = AB^2 + AH^2
CA^2 = 9^2 + 4^2
CA^2 = 81 + 16
CA^2 = 97

5. Затем найдем корень из этого уравнения, чтобы найти CA:

CA = √97, что приближенно равно 9.85.

Таким образом, CA ≈ 9.85.