Выразите a через b из равенства 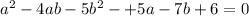
Другие вопросы по теме Математика
Популярные вопросы
- Всвязке 125 шаров.синих шаров в два раза больше чем красных, зеленых...
3 - Написати діалог 7-8 реплік. на тему у магазині ....
3 - Вкакую из перечисленных эпох горообразования сформировалась горная...
3 - Составьте текст из 3-4 предложений про осень ,где дети играют...
2 - Когда речь идёт о возобновляемых природных ресурсах,имеется в...
3 - Пример: вес тела,гравитации перезагрузки...
1 - Мне надо составить 2 придложения рассуждения...
1 - Реши примеры: и раставь правельно дейстивия 40: 8+2*100= 100-(40+36):...
1 - Разложите на простые множители числа 42,58,77,289...
1 - In summer the children dive and swim перевод...
2
(см. объяснение)
Пошаговое объяснение:
Смысл задания в том, чтобы разложить данное выражение на множители. Сделать это можно двумя
1-ый
Понятно, что увидеть это достаточно сложно, поэтому не каждый может пользоваться таким приемом. Для тех, кто не может пользоваться таким методом, есть более длинный, но универсальный алгоритм.
2-ой
Решим данное уравнение относительно a:
Несложно увидеть здесь квадратное уравнение.
Значит решаем через дискриминант:
Теперь воспользуемся формулой разложения квадратного трехчлена на множители:
Пришли к тому же результату. Я рекомендую пользоваться вторым
Теперь несложно получить ответ, если вспомнить, что произведение равно 0, если хотя бы один из его множителей равен 0, а другой при этом не теряет смысла.
Значит:
или
Откуда получаем, что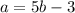 или
или 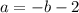 .
.
Задание выполнено!