1. Математика
  2. Вычислите определенные интегралы,

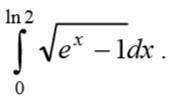
Вычислите определенные интегралы, используя замену переменной.


Вычислите определенные интегралы, используя замену переменной.

DarknEssDk11 DarknEssDk11    2   21.12.2020 20:53    8

Ответы
leanir leanir  20.01.2021 21:07

замена:

{e}^{x} - 1 = t \\ {e}^{x} = t + 1 \\ {e}^{x} dx =dt \\dx = \frac{dt}{ {e}^{x} } = \frac{dt}{t + 1} \\ t1 = {e}^{ ln(2) } - 1 =2 - 1 = 1 \\ t2 = {e}^{0} - 1 = - 1

\int\limits \frac{ \sqrt{t} dt}{t + 1} \\

делаем еще одну замену:

\sqrt{t} = u \\ t = {u}^{2} \\ dt = 2udu

Замену переменных делать не будем, так как один из пределов равен корню из (-1). В Полученный интеграл подставим все замены и тогда найдем численное решение.

\int\limits \frac{u \times 2udu}{ {u}^{2} + 1 } = 2\int\limits \frac{ {u}^{2} }{ {u}^{2} + 1} du = \\ = 2\int\limits \frac{ {u}^{2} + 1 - 1 }{ {u}^{2} + 1} du = \\ = 2\int\limits \: du - 2\int\limits \frac{du}{ {u}^{2} +1 } = \\ = 2u - 2arctg(u) + C= \\ = 2(u - arctg(u)) + c=2(\sqrt{{e}^{x}-1}-arctg(\sqrt{{e}^{x}})+C

подставляем пределы:

2(1-arctg(\sqrt{1})-(0-arctg({\sqrt{-1}}))=\\=2(1-\frac{\pi}{4})=2-\frac{\pi}{2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Imdav88 Imdav88  11.03.2019 08:19
Уайым было 1500 тенге она потратила 4/5 часть этих денег на покупку тетрадей и 1/10 части на покупку карандашей. сколько денег осталась у айым ? решать с подробным решением...
ГЛУПАЯДОМАШКА ГЛУПАЯДОМАШКА  11.03.2019 08:20
Кнаименьшему общему знаменателю дроби: а) 3/8 и 11/16; б)3/8; 5/6 и 1/4; в) 3/14; 4/21 и 5/6. заранее большое ....
yadron54 yadron54  11.03.2019 08:25
Всем номер . желательно сделать на листочке и сфоткать ! 12...
StasyaGolden StasyaGolden  11.03.2019 08:27
Известно, что c и k — отрицательные числа. сравни, используя знак , или =....
Stiv191001 Stiv191001  11.03.2019 08:27
3/4⋅|x|+15,25=−2 (першим запиши менше число)відповідь: x1=x2=...
baby2525 baby2525  11.03.2019 08:27
Решите уравнение 2cos^2x=cosx+3...
ВероникаЛицей124 ВероникаЛицей124  11.03.2019 08:28
Паша,маша и юля решили съесть пиццу. паша съел половину маша 1/5 часть . оставшуюся часть съела юля. какую часть съела юля ? с подробным перешием ​...
daniil6092002 daniil6092002  11.03.2019 08:28
Оцените периметр и площадь прямоугольника со сторонами а см и b см где 4,5≤а≤4,7; 11,1≤b≤11,3...
Lolka200Fantazii0 Lolka200Fantazii0  11.03.2019 08:30
Решите , ^-^ в группе 15 человек изучают язык, 7- французский, 3- . найти вероятность того, что 5 произвольно выбранных студентов изучают язык...
Ulyana2006mizik5B Ulyana2006mizik5B  11.03.2019 08:32
3/4⋅|x|+15,25=−2 (першим запиши менше число) відповідь: x1= x2=...

Популярные вопросы