Вычислить пределы функций, используя i, ii замечательные пределы и эквивалентность бмф.
Другие вопросы по теме Математика
Популярные вопросы
- От чего зависит давление в жидкости?...
2 - Тест по теме: Увертюра-фантазия «Ромео и Джульетта» 1. Кто написал...
3 - Что уникального в панде (2 предложения)...
1 - Чем рост отличается от развития? Привести примеры ....
2 - Отметь все прямые пропорциональности ...
1 - В правильной треугольной призме ABCA1B1C1 Через сторону АВ нижнего...
1 - 1) Что понравилось в рассказе, а что вызывает ваше осуждение? 2)...
3 - Напиши сочинение на тему Необычные герои (В чём заключается их...
2 - Привет ребята нужна ваша Заполни таблицу Социальные группы казахского...
2 - Арман 3 2 ге оқимын деген шынайы ниет болу керек деген....
1
При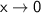
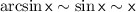 ;
;
Таким образом, можно переписать предел: