Вычислить площадь фигуры,ограниченной линиями: 1) y=-5x; x=3; y=0 2) y=2x в кв; y=0; x=-1; x=9. 3) y=x в кв - 5x+4; y=0

Ответы

blackcat18 17.06.2020 17:21

y = 0 - ось OX
Площадь фигуры будем искать на промежутке [0;3]

Т.к фигура расположена под осью OX, значит площадь фигуры находим по формуле

S =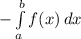 $-\int\limits^b_a {f(x)} \, dx$

Теперь просто подставляем значения

S =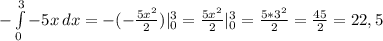 $-\int\limits^3_0 {-5x} \, dx = -(-\frac{5x^2}{2})|_0^3 = \frac{5x^2}{2}|_0^3 = \frac{5 * 3^2}{2} = \frac{45}{2} = 22,5$ ед^2

2) Не совсем понял, решу позже

Парабола пересекает ось OX в точках 1 и 4. Будем искать площадь на промежутке [1;4]

S =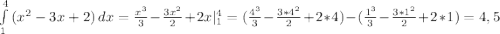 $\int\limits^4_1 {(x^2 - 3x + 2)} \, dx = \frac{x^3}{3} - \frac{3x^2}{2} + 2x|_1^4 = (\frac{4^3}{3} - \frac{3 * 4^2}{2} + 2 * 4) - (\frac{1^3}{3} - \frac{3 * 1^2}{2} + 2 * 1) = 4,5$ ед^2

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

UlnaeMai 08.06.2019 06:10

Найдите значение выражения (18-23)*(-32+28): (-10)...

danchik1106 08.06.2019 06:10

3.решите уравнение: а) 8x-7x+10=13; б) 148-13a=85....

УльянаТонких 08.06.2019 06:10

Отметьте на координатной плоскости точки м(-4; 6), n(6; 1), k(-4; 0), l(2; 6). найдите координаты точки пересечения прямой mn и отрезка kl....

megolodoon 08.06.2019 06:10

5. воднойкоробке8кубиков. всегонаполке60такихкоробок. ? 6. 75 кг меда разлили в 15 одинаковых банок. сколько меда в 9 таких банках...

Gohanhik 08.06.2019 06:10

Радиус переднего колеса кареты равен 0,25 м, а заднего 0,6 м. какое расстояние проехала карета, если ее заднее колесо сделало на 280 оборотов меньше, чем переднее?...

боня51 08.06.2019 06:10

Постройте прямоугольник со сторонами ав = 4см, аd = 7см. проведите луч аl, пересекающий сd в точке l так, чтобы угол dal оказался равным 25 градусов.выполните необходимые измерения...

DmitryKind98 08.06.2019 06:10

Какие животные могут быть карликовыми....

irynasherem02 08.06.2019 06:10

Решить : два поезда идут навстречу друг другу. скорость одного из них 80 км/ч, а скорость второго в одну челую одну седьмую раза меньше. через сколько они времени встретятся, если...

Chundokova 08.06.2019 06:10

Найдите значение выражения 0.9*(-0.2)-0.6*(-0.2) (2/9-5/6)*(0.36: 0.02) , 2/9 и 5/6-это дроби...

zahar4ikk 08.06.2019 06:10

1) выражение: выражение: -(m-3,8)+(4,8+m) 2) решите уравнение : a) 0,6(x+7)=0,5(x-3)+6,8 3) на первой стоянке в 4 раза меньше автомашин, чем на второй. после того как на первую...

Вычислить площадь фигуры,ограниченной линиями: 1) y=-5x; x=3; y=0 2) y=2x в кв; y=0; x=-1; x=9. 3) y=x в кв - 5x+4; y=0

Популярные вопросы