Вычислить определенный интеграл по формуле Ньютона-Лейбница 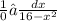
Другие вопросы по теме Математика
Популярные вопросы
- Задания 1. На рисунке представлена экосистема. (а) Используя данную экосистему,...
2 - Написати твір на тему; Як я долаю труднощі будь ласка до іть!!...
3 - Відкрити дужки в Present Perfect I can t use my phone because I (forget)...
2 - ДО ІТЬ «Буба: мертвий сезон» 1. Про події в творі розповідає….. 2. З усієї...
1 - =( ответ скринами из программы...
1 - Частота електромагнітних коливань в контурі 64 МГц. Ємність конденсатора...
3 - . Разложите многочлен на множители: 15²с -3a²+5ac² - ac...
2 - Лабораторна робота № 1 Визначення електроємності конденсатора за до гальванометра...
3 - Використовуючи спеціальний клас TCanvas, написати програму для малювання...
2 - 1. I m so hungry. I think I ll make 2. Please help 3. I m surprised they...
2
Пошаговое объяснение: