Вычислить объем тела, ограниченного поверхностями
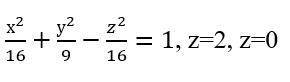
Другие вопросы по теме Математика
Популярные вопросы
- Вскобках семь восьмых минус 0,2 скобка закрывается умножить на икс...
1 - Решите неравенство: (|x|-3)(|x|+7) 0...
3 - Прочитайте слова и скажите, какой частью речи является выделенное цветом...
3 - Вырази в тоннах и килограммах 1000032 кг...
1 - Автотуристы проехали 240 км проехали каждый час 80 км а потом 420 проехали...
3 - Решение на проценты пропорции на сколько % увеличится площадь квадрата,если...
2 - Составьте 2 предложений на тему как я провёл лето с использованием...
1 - До какой температуры нагреется вода объемом 4 л, если она получит 126...
2 - Составьте словосочетания по следующим схем: 1)глагол+существительное...
2 - Le roi de france, philippe auguste, fait construire une forteresse...
3
Пошаговое объяснение:
здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности
1 страшная формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
запишем наш эллипс
теперь нам надо каноническое уравнение нашего эллипса
упростим
площадь этого замечательного гиперболоида вычисляется по формуле
S=πab
у нас
отсюда
S=π*(3/4)(16+z²)
вот, собственно, и все "загогулины"
остался только объем