вычислить длину линии, ограниченной астроиды x=3cos^3(t), y=3sin^3(t) На рисунке изобразил задание. Выписал формулу, нашел обе производных только с нахождением определенного интеграла. (На рисунке все написано правильно). За ранее !
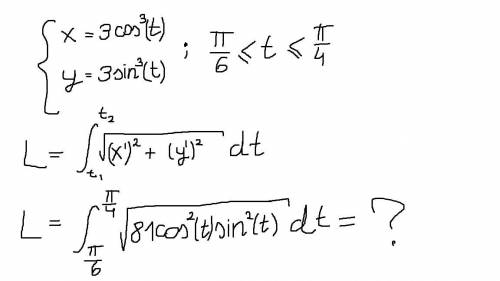
Другие вопросы по теме Математика
Популярные вопросы
- с двумя заданиями у меня контрольная за год как можно быстрей...
3 - Https://video.ibm.com/channel/yDbMdtLyJ5C...
1 - Для обработки рудных ископаемых применяются разные методы. напиши названия...
2 - Определите количество натуральных чисел от 1 до 2016, которыеодновременно...
3 - Тест на тему «Лыжная подготовка» 1. К циклическим видам спорта относятся...:...
1 - Построить график функций у=х(4-х)...
1 - Письменно текст выступления о необходимости охранять природу с использованием...
1 - В первый день в магазине продали 150 кг яблок, составило 3/5 всех привезённых...
3 - Почему в конце текста Толя вдруг махнул рукой и поднял гордо голову бодро...
2 - Приведи подобные слагаемые (a в квадрате + 2a+2a+4). Это учи ру если что...
1
ответ:1,125
Пошаговое объяснение:I=∫ₙ₍₆ⁿ⁽⁴ 9·|Cost|·|Sint|dt=
т.к. π/6≤t≤π/4, то Sint≥0, Cost≥0 ⇒ |Cost|=Cost , |Sint|=Sint
=∫ₙ₍₆ⁿ⁽⁴ 9·Cost·Sint dt=∫ₙ₍₆ⁿ⁽⁴ 4,5· (2Cost·Sint) dt=4,5∫ₙ₍₆ⁿ⁽⁴ Sin (2t)dt=
=2,25·∫ₙ₍₆ⁿ⁽⁴ Sin (2t)d(2t)= - 2,25 ·Cos(2t) |∫ₙ₍₆ⁿ⁽⁴=
=- 2,25·(Cos π/2 - Cos π/3)= -2,25 ·(0-0,5)=1,125