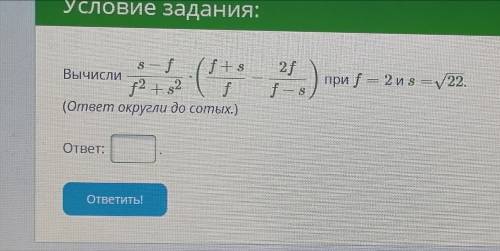
Вычисли s−ff2+s2⋅(f+sf−2ff−s) при f=2 и s=22−−√.
(ответ округли до сотых.)
Другие вопросы по теме Математика
Популярные вопросы
- Послетого, , весящика сконфетамиуменьшилсяна45 %. определите массу...
1 - Вкаком варианте ответа правильно указаны все цифры на месте которых...
2 - Постав те скобки 9664/32-2*195-37*5=3000...
1 - Счего начинается патриотизм и в чем он выражается....
3 - Вкаких веках существовало государство газневидов? а) в x-xi вв. б)...
3 - Обж,5 класс доклад по скользкому звонкому льду надо сегодня...
2 - 1)плавательный пузырь отсутствует у 1) осетра 3)акулы 2)леща 4)форели...
1 - Сравнительный анализ стихотворений тютчева гроза и заболоцкого гроза...
2 - Пояснити значення прислів*я слово- не горобець , вилетить не спіймаєш...
3 - Що таке фонетика - що таке теза - що таке синтаксис - що таке висновок...
2
це правильно сто відст.
Шаг 1: Подставим значения f=2 и s=22−−√ в выражение s−ff2+s2⋅(f+sf−2ff−s)
Заменим f на 2 и s на 22−−√ в выражении:
s−ff2+s2⋅(f+sf−2ff−s) = 22−−√−2(2)2+22−−√2⋅(2+22−−√−22−−√) = 22−−√−4+22−−√4⋅(2+22−−√−22−−√)
Шаг 2: Раскроем скобки внутри выражения s2⋅(f+sf−2ff−s)
Умножим s2 на каждый элемент в скобках:
s2⋅(f+sf−2ff−s) = (22−−√)2⋅(2+22−−√−22−−√) = (22−−√)2⋅(2+22−−√−22−−√) = 44−−√−4⋅(2+22−−√−22−−√)
Шаг 3: Упростим выражение s−ff2+s2⋅(f+sf−2ff−s)
Скомбинируем все элементы вместе:
s−ff2+s2⋅(f+sf−2ff−s) = 22−−√−4+44−−√−4⋅(2+22−−√−22−−√) = 22−−√−4+88−−√−8+4⋅22−−√−2⋅22−−√ = 22−−√−4+88−−√−8+8⋅22−−√−4 = 22−−√−4+88−−√−8+16−−√−8 = 22−−√+88−−√+16−−√−20
Шаг 4: Округлим ответ до сотых
Итак, ответ равен 22−−√+88−−√+16−−√−20. Это десятичное число, мы можем округлить его до ближайшей сотой:
22−−√ ≈ 1.41
88−−√ ≈ 2.83
16−−√ ≈ 4.00
Используя эти округленные значения, мы можем снова рассчитать наш ответ:
22−−√+88−−√+16−−√−20 ≈ 1.41+2.83+4.00−20 ≈ -11.76
Таким образом, приближенный ответ на данный вопрос округляется до -11,76 до сотых.