1. Математика
  2. Вычеслить предел lim

Вычеслить предел lim числитель 2х знаменатель/ под корнем 4+х -2

апрркн1 апрркн1    1   27.05.2019 05:30    0

Ответы
Даниил358 Даниил358  23.06.2020 22:16
Правило лапиталя своими словами: предел отношения функций равен пределу отношений их производных

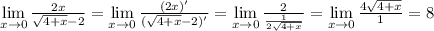
\lim\limits_{x\to 0} \frac{2x}{ \sqrt{4+x}-2 }= \lim\limits_{x\to 0} \frac{(2x)'}{( \sqrt{4+x}-2)' }=\lim\limits_{x\to 0} \frac{2}{ \frac{1}{ 2\sqrt{4+x} } }=\lim\limits_{x\to 0} \frac{4\sqrt{4+x}}{ 1}=8
ПОКАЗАТЬ ОТВЕТЫ
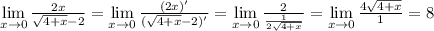
Другие вопросы по теме Математика
Женьочки Женьочки  21.08.2019 18:30
Из города в одновременно в одном отправления выехали автомобиль и и велосипедис. скорость автомобиля 80 км/час, а велосипедист 50 км/час. какое расстояние будет между ними...
PomoGayka0 PomoGayka0  21.08.2019 18:30
Спервого участка собрали 1720 кг моркови со второго в 3 раза больше чем с первого а с третьего на 3098 кг меньше чем с первого и второго участка в месте сколько килограммов...
лсагамлснс лсагамлснс  21.08.2019 18:30
Рассмотрите файловую структуру диска на котором записаны работы участников...
Frororo Frororo  21.08.2019 18:30
15 7/15 - 5 13.15 выполните вычитание...
luizazamanov luizazamanov  21.08.2019 18:30
1)периметр квадрата равен 18(целых) 2/5 см. найдите длину стороны квадрата . 2)сумма всех рёбер куба равна 69 см. найдите длину ребра куба . ....
Александра102854321 Александра102854321  21.08.2019 18:30
Иеще подскажите построй квадрат периметр которого в 2 раза больше периметра квадрата имеющего площадь 4кв.см....
Dikaya24 Dikaya24  21.08.2019 18:30
Короткое плечо колодца с журавлём имеет длину 1,5 м а длинное плечо 3 м.на сколько метров опустится конец длинного плеча,когда конец короткого поднимется на 0,4 м?...
Loomina Loomina  21.08.2019 18:30
Начерти прямоугольник со сторонами 6 см и 4 см . найди его пириметер и площадь.отметь и закрась одну третью площади прямоугольника...
daridasha57ү daridasha57ү  21.08.2019 18:30
Впарк пришли 29 человек и расселись на 12 лавочек, причём на некоторых лавочках сидели по-двое, а на остальных по-трое. на скольких лавочках сидели по два человека? решите...
ЯМС ЯМС  21.08.2019 18:30
Вынесите общий множитель за скобки: 1/4*12/25+5/6*12/25; 15/28*2/3-15/28*1/5; 1/8*4/11-1/10*4/11+1/4*4/11; 18/49*1/3-18/49*1/9+1/6*18/49;...

Популярные вопросы