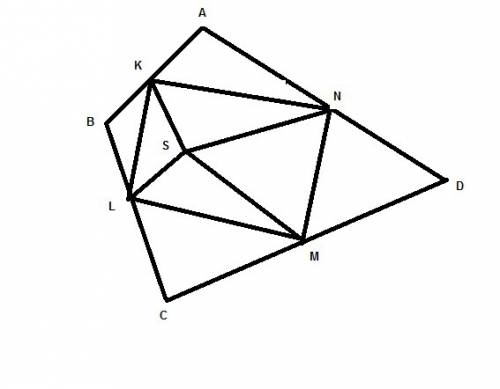
Ввыпуклой четырехугольнике abcd точка к - середина ав, точка l - середина вс, точка м - середина сd, точка n - середина da. для некоторой точки s, лежащей внутри четырехугольника abcd, оказалось, что ks=ls и ns=ms. докажет, что угол ksn=углу msl , )
Ответы
Для треуг-ка АВD прямая KN является средней линией, значит она параллельна диагонали BD. Для треуг-ка BCD отрезок LM является средней линией и он тоже параллелен диагоналиBD. Значит KN и ML параллельны. Аналогично KLпараллельна MN. То есть KLMN это параллелограмм. Треугольники KSN и LSM равны ( по трем сторонам), поэтому углыKSN иMSL равны
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика
Популярные вопросы
- Сравните числа 1) 3.1 и -6.7 2) -4.2 и -4.6 Посчитайте: 1) |-7.3| +...
3 - Составьте пословицы подобрав их части ...
3 - *Решить уравнение 1) ㏑ x = ㏒7 (ln 3x); 2) sin x + cos x + tg x + ctg...
2 - Тема нашествие персидских войс конспект Желательно в крации)...
3 - Я Самира и я живу в Казани...
2 - За якої температури повітря з абсолютною вологістю 5г/м3 буде насиченим...
3 - На какой вопрос отвечает слово доклад? ...
2 - 1991-2020 жылдар аралығында Қазақстанда не болғанын қанадай заң қабылдағанын...
1 - Как образовался казахский ханства ...
3 - Випишіть із художніх творів чотири речення,у яких є слова з префіксами...
3