Все отдам 4)х^2+7ху=-6 9у^2-ху=10
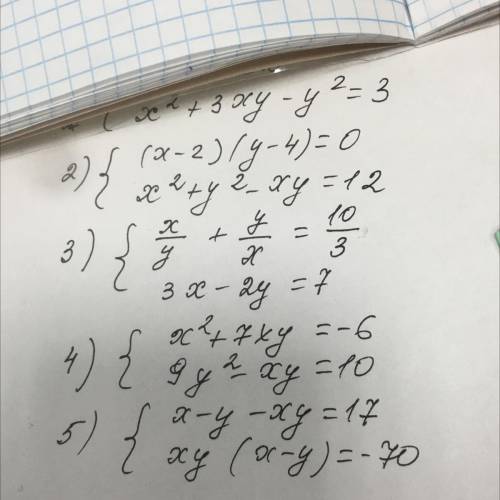
Другие вопросы по теме Математика
Популярные вопросы
- 1.отношения между людьми, возникающие по поводу имущества: 1) имущественные...
2 - Вычислить объем тетраэдра с вершинами в указанных точках и его высо-ту, опущенную...
3 - Нужно сочинение для 3 класса: у саши папа заядлый грибник!...
3 - Напишите сочинение на тему « мой класс»сделайте большим ! 30...
2 - Туристы отправились в трёхдневный поход.сколько кг хлеба потребуется туристам...
2 - Найбільшу кількість електрики, яку одержують під час розряджання акумулятора...
3 - Прочтите отрывок из источника и укажите событие, о котором идёт речь. «и...
2 - Вставьте пропущенные буквы, графически объясните орфограммы.выр_сти, выр_сший,...
2 - словообразования : издалека, прославить, пароходный, написать....
3 - Точка c - середина отрезка ab, точка o - середина отрезка ac. найдите ao,...
2
1. Давайте начнем с первого уравнения: 4x^2 + 7xy = -6. Мы можем выразить x через y, чтобы иметь одну переменную:
4x^2 = -7xy - 6
x^2 = (-7xy - 6) / 4
x = sqrt[(-7xy - 6) / 4] (корень квадратный)
2. Теперь, когда у нас есть выражение x через y, мы можем его подставить во второе уравнение: 9y^2 - xy = 10:
9y^2 - sqrt[(-7xy - 6) / 4] * y = 10.
Теперь мы имеем уравнение только с одной переменной - y.
3. Давайте продолжим решать это уравнение. Мы можем упростить уравнение, перенеся все члены в одну сторону:
9y^2 - sqrt[(-7xy - 6) / 4] * y - 10 = 0
4. Теперь мы можем использовать квадратное уравнение для нахождения значения y.
Для удобства вместо sqrt[(-7xy - 6) / 4] обозначим это выражение как a:
9y^2 - ay - 10 = 0
5. Решим это уравнение с помощью формулы дискриминанта. Формула дискриминанта имеет вид:
D = b^2 - 4ac
Где a = 9, b = -a и c = -10. Подставим значения и найдем D:
D = (-a)^2 - 4 * 9 * (-10)
D = a^2 + 360
6. Теперь найдем значение y с помощью формулы корней квадратного уравнения:
y = (-b +/- sqrt(D)) / (2a)
Подставим значения и найдем y:
y = (a +/- sqrt(a^2 + 360)) / (18)
7. Теперь, когда у нас есть значения y, мы можем использовать их, чтобы найти соответствующие значения x с помощью выражения x = sqrt[(-7xy - 6) / 4].
Подставьте найденные значения y в это выражение и получите значения x.
Таким образом, решение данной системы уравнений состоит из двух корней (x, y). Вы можете проверить их, подставив их обратно в исходные уравнения и убедившись, что они верны.