Всё дано в картинках, НАЙТИ НУЖНО Sбок.цил.
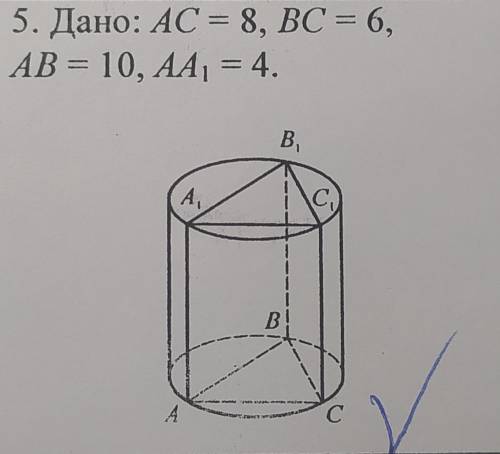
Другие вопросы по теме Математика
Популярные вопросы
- Определите степень окисления хрома в соединении k2 cr2 o7...
1 - Осевое сечение конуса – равнобедренный треугольник с углом 120˚ и равными сторонами...
1 - Сочинение-описание форфоровой куклы для 6 класса. ! буду !...
2 - Как называется растение которое оканчивается на букву я ?...
2 - Решите уравнение tgx плюс 1 равно 0 и запишите в градусах любой его корень.....
2 - Дано два массива х (n) у (n) .найти среднее арифметическое положительных элементов...
2 - Втрёх товарных ваготах можно перевести руз массой 50 тонн. сколько тонн груза...
3 - Решите уравнение: 1) (x+5)³-(x+1)³=4(3x²-5) 2) (y+4)³+(3y+1)³-7y²(4y+9)=-24y²+8...
3 - Поставь указанные имена существительных в указанном падеже дервня(д.п) сирень(т.п)...
1 - Определите оптическую силу объектива проекционного аппарата, если он дает 24-кратное...
1
ответ: 160π см²; 16π см²; 40π см²
Пошаговое объяснение:
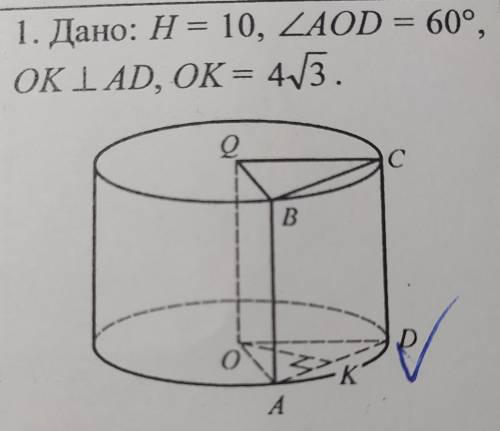
1. Площадь боковой поверхности цилиндра равна произведению длины основания цилиндра на его высоту:
S=L*h
L=2*π*ОА
ОА=ОК/cos ∠AOD/2=4√3/cos30°=8см
S=2*π*8*10=160π cм²
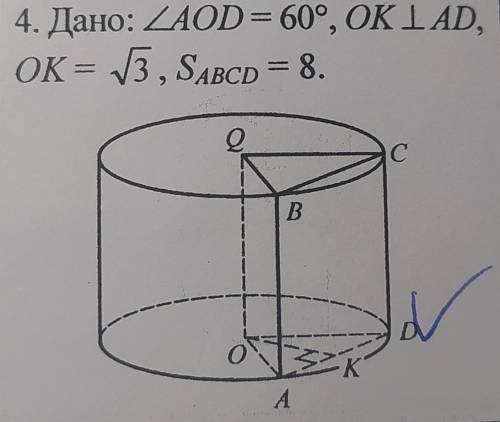
2. S=L*АВ
L=2π*ОА
ОА=ОК/cos∠AOD/2=√3/(√3/2)=2см
АВ=Sabcd/AD
AD=OA*(sin∠AOD/2)*2=2*0,5*2=2см
АВ=8/2=4см
S=2*π*ОА*АВ=2*π*2*4=16π см²
3 S=2πR*AA1
R=abc/(4√p(p−a)(p−b)(p−c))р=(АВ+ВС+АС)/2=(8+6+10)/2=12см
R=8*6*10/(4√12*(12-8)*(12-6)*(12-10))=480/96=5cм
S=2*π*5*4=40π cм².