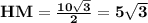В треугольнике ABC точка О - центр вписанной в треугольник окружности. Прямая ВО пересекает сторону АС в точке Н, прямая АО пересекает сторону ВС в точке М. уголВНС=углуАМС=90°. 1) Докажите, что треугольник АВС равносторонний
2) Найдите HM, если ОМ=5
!

2) HM=5√3

Пошаговое объяснение:

1)              Доказательство:

Угол, который образовался между прямыми и противолежащими сторонами равен 90°, тогда прямые перпендикулярны и являются высотами, проведём 3-ю высоту СК ,которая опущенна на сторону АВ. О-точка пересечения высот, и не только, также биссектрисы и медианы, биссектриса делит углы пополам, а если О-точка пересечения биссектрис, тогда AO=BO=CO ⇒ ∠CBO=∠CBA, ∠BCO=∠ВCH. ∠CAO=∠СAK ⇒∠АВС=∠ВСА=∠САВ , значит , АВ=ВС=СА(все стороны равностороннего треугольника равны) . ΔАВС-равносторонний.

      Доказано!

2)  (см. чертёж)

HM является средней линией , средняя линия это -отрезок , соединяющий середины двух сторон.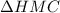 ~ 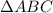= 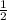(треугольники подобны по свойству средней линии , а коэффициент пропорциональности  1 к 2 ) значит , ΔHMC<ΔАВС в 2 раза , тогда аногологично , что НМ<АВ в 2 раза ,  найдём стороны большего ΔАВС , а стороны подобного , маленького ΔНМС в 2 раза будут меньше , чем и является НМ.  OM=r - радиус окружности ,  АВ=ВС=СА=а - равная длина всех сторон , если равносторонний треугольник описан около окружности - то  можно из формулы 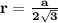найти а ,подставим известные данные и найдём а.

Значит