В равнобедренном треугольнике абс основание ас=28 аб=бс tg A= 10_7 Найдите площадь треугольника абс

Ответы

minis551 15.10.2020 14:30

Проведём высоту BH. Высота BH одновременно является медианой и биссектрисой. AH = HC = AC/2 = 14. Площадь треугольника: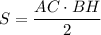 $S=\dfrac{AC\cdot BH}{2}$ . Рассмотрим прямоугольный треугольника ABH:

${\rm tg}\, A=\dfrac{BH}{AH}=\dfrac{AC\cdot BH/2}{AC^2/4}=\dfrac{4S}{AC^2}~~\Leftrightarrow~~\dfrac{10}{7}=\dfrac{4S}{28^2}~~\Rightarrow~~ S=280$

ПОКАЗАТЬ ОТВЕТЫ

marehkolia2343Apple 12.01.2024 04:48

Для решения этой задачи, нам понадобится использовать несколько свойств и формул, связанных с треугольниками и тригонометрией. Давайте разберемся по шагам:

1. Первое, что мы можем заметить в условии задачи - это равенство длин оснований ас и бс(аб=бс). Это означает, что угол а в этом треугольнике равен углу б. Так как треугольник равнобедренный, у него также равны основания и высоты, которые опущены из вершин а и б на основание с. Давайте это запишем:
ас = бс = 28 (дано)

2. У нас также есть информация о тангенсе угла А, который составляет 10/7 (tg A = 10/7). Мы можем использовать это для нахождения значения самого угла А, используя обратную функцию тангенса (арктангенс). Подставим значение тангенса и выпишем арктангенс:
A = arctan(10/7) (находим угол А)

3. Теперь, когда у нас есть значение угла А и мы знаем, что угол а равен углу б, мы можем использовать формулу для нахождения площади треугольника. Формула для площади треугольника, в которой известны длины двух сторон и синус угла между этими сторонами, выглядит следующим образом:
S = (a * b * sin(C)) / 2
где S - площадь треугольника, a и b - длины сторон, C - угол между этими сторонами.

4. Мы знаем, что сторона ас и сторона бс равны 28, а угол А равен углу Б (по условию задачи), значит у нас есть основание треугольника. Также у нас есть значение угла А (полученное во втором шаге).

5. Остается найти значение синуса угла А. Мы можем использовать различные формулы для нахождения синуса, в зависимости от того, какая информация нам известна о треугольнике. В нашем случае, мы можем использовать теорему синусов для нахождения синуса угла А:
sin(A) = a / c
где с - гипотенуза треугольника. В нашем случае, если мы проведем прямую из вершины а (или б) перпендикулярно к линии с, мы поймем, что с - основание треугольника ас (или бс), а c - высота треугольника (так как треугольник равнобедренный, высота будет проведена из середины основания с, по середине аб). Так как треугольник равнобедренный, высота с будет одновременно и медианой, разделяющей основание на две равные части.

6. Таким образом, мы можем сказать, что высота с равна половине основания ас (или, что равносильно, половине основания бс):
c = as / 2 = bs / 2 = 28 / 2 = 14 (высота треугольника с)

7. Теперь, когда у нас есть значения основания ас и синуса угла А, мы можем подставить их в формулу для площади треугольника, чтобы найти искомое значение:
S = (as * cs * sin(A)) / 2
S = (28 * 14 * sin(A)) / 2

8. Полученное значение площади - это ответ на вопрос, который был задан в задаче: площадь треугольника абс.

Вот и все. Надеюсь, что данное решение поможет вам разобраться в задаче и получить верный ответ. Если остались какие-либо вопросы, обязательно спрашивайте!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика