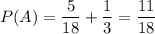В первой урне 6 белых и 6 черных шаров, во второй урне 3 белых и 5 черных шара. Из первой урны взяли 1 шар и переложили во вторую урну, после этого из второй урны взяли 1 шар. Найти вероятность, что этот шар черный
Другие вопросы по теме Математика
Популярные вопросы
- Ідея новели «Останній листок»... * мистецтво здатне творити дива уславлення дружби...
1 - За до пошукових систем знайдіть в Інтернеті інформацію про те, які професіїє найбільш...
3 - Знайти видовження пружини жорсткістю 80 H/м, потенціальна енергія якої 300 Дж...
3 - Розв язати нерівністьlog2x 5...
1 - ORA ORA ORA ORA ORA ORA ORA ORA ORA ORA ORA ORA...
2 - Қазақтың ұлттық ою-өрнектері Лепті сөйлемді анықта.ою-өрнектердің бояуын қанық...
3 - Чому дорівнює момент сили другого плеча врівноваженого важеля, якщо до другого...
3 - Complete the sentences with the passive form of the verbs in blackets...
2 - основа рівнобедриного трикутника дорівнює 4см а бічна сторона 8см .Знайдіть висоту...
2 - Знайдіть площу рівнобічної трапеції з основами 12 та 18 см та тупим кутом 135 градусів....
3
A — из первой урны переложили шар во вторую и затем из второй урны взяли шар и им оказался чёрный шар.
B₁ — переложен белый шар
В₂ — переложен черный шар.
Белый шар из первой урны переложим с вероятностью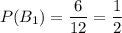 . Во второй урне будет 4 белых и 5 черных шара. Тогда вероятность извлечения чёрного шара из второй урны равна
. Во второй урне будет 4 белых и 5 черных шара. Тогда вероятность извлечения чёрного шара из второй урны равна 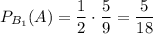 . Аналогично, чёрный шар из первой урны достаём с вероятностью
. Аналогично, чёрный шар из первой урны достаём с вероятностью 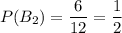 . Тогда вероятность извлечения чёрного шара из второй урны равна
. Тогда вероятность извлечения чёрного шара из второй урны равна 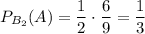 .
.
Искомая вероятность: