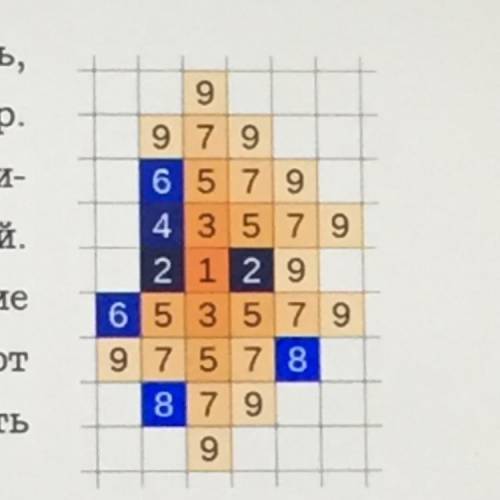
В городе, представляющее собой бесконечную клетчатую плоскость, есть n пожарных. Однажды в одной из клеток города возникает пожар. В Следующую минуту каждый пожарный может ( но не обязан) защитить какую-нибудь одну еще не горящую клетку, соседнюю с горящей. Ещё через минуту пожар распространяется на все клетки, соседние с горящими, кроме защищенных. Далее пожарные и пожар действует по очереди. При каком минимальном n пожарные смогут локализовать пожар, то есть сделать так, чтобы он перестал распространяться? (на рисунке показано, как могут развиваться события при n=2; Нечетное число соответствует распространению пожара, а чётные – действиям пожарных).

sashawinner13    1   04.11.2021 17:42    189