В четырехугольной пирамиде SABCD основание – квадрат ABCD. Ребро SA перпендикулярно плоскости основания. SB =10, AB =8.

а. Найдите тангенс угла наклона ребра SC к плоскости основания.

б Найдите тангенс угла плоскости (SCB) к плоскости основания.

в Найдите объем данной пирамиды.

г Найдите площадь полной поверхности.

Ответы

erkinsultanov 05.04.2022 03:49

а. Тангенс угла наклона ребра SC к плоскости основания равен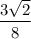 $\displaystyle \frac{3\sqrt{2} }{8}$ ;

б. Тангенс угла плоскости (SCB) к плоскости основания равен $\displaystyle \frac{3}{4}$ ;

в. Объем данной пирамиды равен 128 ед.³

г. Площадь полной поверхности равна 192 ед.²

Пошаговое объяснение:

Требуется найти:

а. Тангенс угла наклона ребра SC к плоскости основания.

б. Тангенс угла плоскости (SCB) к плоскости основания.

в. Объем данной пирамиды.

г. Площадь полной поверхности.

Дано: SABCD - пирамида;

ABCD - основание, квадрат;

SA ⊥ ABCD;

SB = 10; AB = 8.

Найти:

а. Тангенс угла наклона ребра SC к плоскости основания.

б. Тангенс угла плоскости (SCB) к плоскости основания.

в. Объем данной пирамиды.

г. Площадь полной поверхности.

Прежде чем приступить к заданиям, нам надо найти высоту SA и диагональ основания АС.

1. Рассмотрим ΔASB.

Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой лежащей в этой плоскости.

⇒ ΔASB - прямоугольный.

По теореме Пифагора:

AS² = SB² - AB² = 100 - 64 = 36

AS = √36 = 6.

2. Диагональ квадрата найдем по формуле:

d = a√2, где а - сторона квадрата.

АС = АВ*√2 = 8√2

Выполним задания:

а. Найдем тангенс угла наклона ребра SC к плоскости основания.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

SA ⊥ ABCD (условие)

⇒ АС - проекция SC на плоскость ABCD.

∠SCA - угол наклона ребра SC к плоскости основания.

Тангенс угла - это отношение противолежащего катета к прилежащему.

$\displaystyle tg\angle{SCA}=\frac{SA}{AC}=\frac{6}{8\sqrt{2} } =\frac{3}{4\sqrt{2} }=\frac{3\sqrt{2} }{8}$

б) Найдем тангенс угла наклона плоскости (SCB) к плоскости основания.

Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Линия пересечения у нас СВ.

Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

СВ ⊥ АВ (ABCD - квадрат)

⇒ CB ⊥ SB.

Искомый угол АВS.

$\displaystyle tg\angle{ABS}=\frac{SA}{AB}=\frac{6}{8}=\frac{3}{4}$