В 3 найдите неопределенный интеграл и сделайте проверку
Другие вопросы по теме Математика
Популярные вопросы
- Решите Уверен носителям будет очень...
1 - построить схему предложения, объясняющую постановку знаков препинания. На...
1 - Гостро сатиричним твором, в якому автор виступає проти Берестейськоїунії...
2 - За промежуток времени =10 точка половину окружности радиуса R = 150 см....
1 - Знайдіть висоту рівнобедреного трикутника, якщо радіус кола, вписаного в...
3 - Задание 1 Раскройте скобки в предложениях, согласно правилу условного предложения...
2 - Твір за темою Твір про любов до ближнього...
2 - Які є корисні копалини в Україні...
1 - Метою хрестових походів було звільнення міста:...
1 - ЕСЛИ ВСЕ РЕШИТЕВариант 21. Составьте уравнения реакций по схемам. Укажите...
3
1)
Проверка: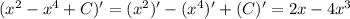
2)
Проверка: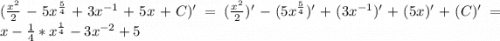
3)
Проверка: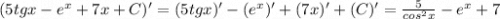
4)
Проверка: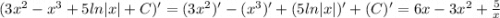
(за место a и b ничего не ставь, т.к у тебя неопределённый интеграл, просто не пиши их)