УМОЛЯЮ РЕШИТЕ РЧЕНЬ НАДО​ ХОТЯ БЫ ОДНО

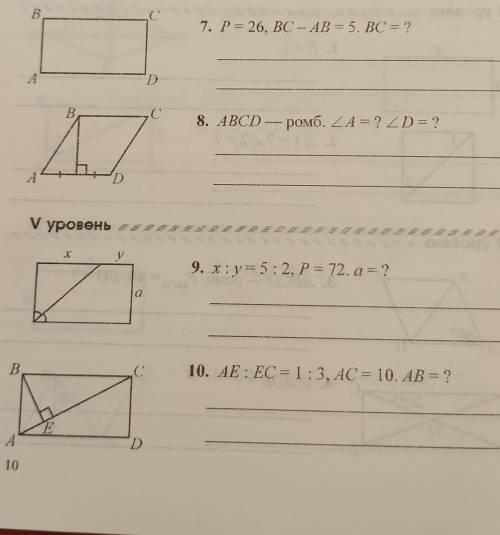
9) Из заданного соотношения х/у = 5/2 находим у = 2х/5.

Полупериметр прямоугольника равен 72/2 = 36.

С другой стороны он равен х + (х + у) = 2х + у = 2х + (2х/5).

Приравняем:  2х + (2х/5) = 36.

Приведём к общему знаменателю.

10х + 2х = 180   или 12х = 180, отсюда х = 180/12 = 15.

По свойству биссектрисы прямого угла имеем а = х.

ответ: а = 15.

10) Используем свойство высоты из прямого угла: АЕ/ВЕ = ВЕ/ЕС.

Так как ЕС = 3АЕ, то АЕ/ВЕ = ВЕ/3АЕ.

Отсюда ВЕ² = 3АЕ².

По Пифагору находим:

АВ = √(АЕ² + ВЕ²) = √(АЕ² + 3АЕ²) = √(4АЕ²) = 2АЕ.

АЕ = 10/4 = 2,5, тогда АВ = 2*2,5 = 5.

ответ: АВ = 5.