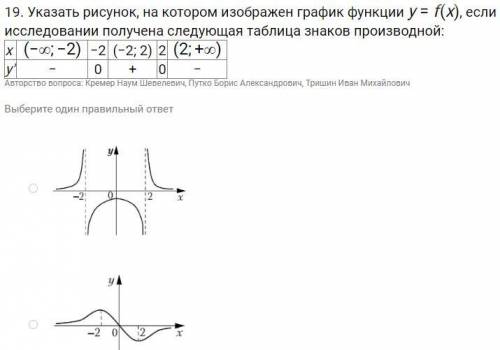
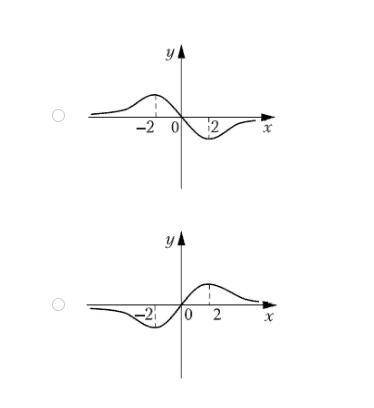
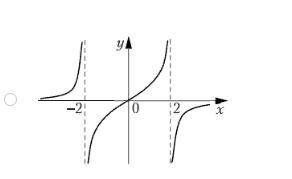
Указать рисунок, на котором изображен график функции y=f(x), если при исследовании получена следующая таблица знаков производной:

Для решения этой задачи мы должны анализировать знаки производной функции y=f(x), которая, вероятно, является гладкой и непрерывной. Займемся этим шаг за шагом:

1. Дано, что f'(x) >0, когда x < -2.
Знак "+" означает, что производная положительна, что в свою очередь говорит нам о том, что функция f(x) возрастает в этом интервале. Чтобы привязать это к графику, мы можем нарисовать некоторую кривую, которая соответствует возрастанию функции при x < -2. Исходя из таблицы знаков производной, можно предположить, что график возрастает, когда x < -2.

2. Дано, что f'(x) <0, когда -2 < x < 0.
Знак "-" означает, что производная отрицательна, что в свою очередь говорит нам о том, что функция f(x) убывает в этом интервале. Чтобы привязать это к графику, мы можем нарисовать некоторую кривую, которая соответствует убыванию функции при -2 < x < 0. Исходя из таблицы знаков производной, можно предположить, что график убывает, когда -2 < x < 0.

3. Дано, что f'(x) >0, когда 0 < x < 3.
Знак "+" означает, что производная положительна, что в свою очередь говорит нам о том, что функция f(x) возрастает в этом интервале. Чтобы привязать это к графику, мы можем нарисовать некоторую кривую, которая соответствует возрастанию функции при 0 < x < 3. Исходя из таблицы знаков производной, можно предположить, что график возрастает, когда 0 < x < 3.

4. Дано, что f'(x) <0, когда x > 3.
Знак "-" означает, что производная отрицательна, что в свою очередь говорит нам о том, что функция f(x) убывает в этом интервале. Чтобы привязать это к графику, мы можем нарисовать некоторую кривую, которая соответствует убыванию функции при x > 3. Исходя из таблицы знаков производной, можно предположить, что график убывает, когда x > 3.

Теперь, когда мы проанализировали каждый интервал и определили направление движения функции в каждом из них, мы можем объединить все кусочки графика в единое целое.
На основании всей предоставленной информации и таблицы знаков производной, мы можем сказать, что график функции y=f(x) должен выглядеть следующим образом:

1. График возрастает, когда x < -2.
2. График убывает, когда -2 < x < 0.
3. График возрастает, когда 0 < x < 3.
4. График убывает, когда x > 3.

Таким образом, график функции y=f(x) должен иметь участки, которые соответствуют возрастанию и убыванию функции в указанных интервалах. График может выглядеть как плавная кривая, которая переходит из возрастающего в убывающий режим и наоборот.