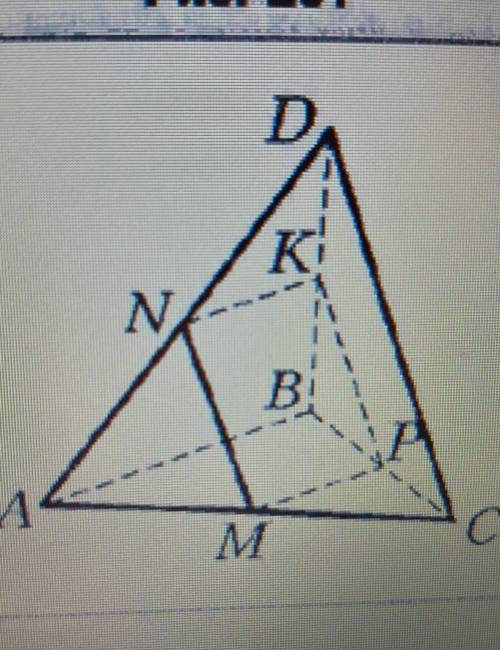
Точки М, N, К и Р — середины рёбер АС, AD, BD и ВС тетраэдра DABC соответственно, АВ = 30 см, CD = 26 см (рис. 107). Докажите, что точки М, N, К и Р являются вершинами параллелограмма, и вычислите периметр этого параллелограмма​

Для доказательства того, что точки М, N, К и Р являются вершинами параллелограмма, нам необходимо показать, что противоположные стороны параллелограмма равны и параллельны.

Для начала, построим необходимые отрезки и точки.

Обратимся к рисунку. Мы видим, что точки М и N соединены отрезком MN, а точки К и Р соединены отрезком КР.

Доказательство:

Шаг 1: Докажем, что АМ = АН и КН = МР.
Поскольку М - середина ребра AD, а N - середина ребра AC, то по свойству серединных перпендикуляров AM = AN (оказывается, что эта теорема называется "теоремой о серединном перпендикуляре").

Аналогично, поскольку К - середина ребра BC, а Р - середина ребра CD, то по свойству серединных перпендикуляров КН = МР.

Шаг 2: Докажем, что MN || КР и АМ = МР.
Так как точки M и N - середины ребра AD и AC соответственно, а точки К и Р - середины ребра BC и CD соответственно, то по свойству серединного перпендикуляра прямые MN и КР являются параллельными (также вытекает из теоремы о серединном перпендикуляре).

Кроме того, AM = МР по доказанному в Шаге 1.

Шаг 3: Докажем, что АМ || МР и АК = МН.
Поскольку AM = МР (по Шагу 2) и АМ = АН (по Шагу 1), то по транзитивности равенства АН = МР.

Также, АК = KN (по теореме о серединном перпендикуляре).

Аналогично, поскольку точки К и Р являются серединами ребра BC и CD соответственно, то АК || МН (также вытекает из теоремы о серединном перпендикуляре).

Таким образом, мы доказали, что точки М, N, К и Р образуют параллелограмм.

Периметр параллелограмма: Теперь вычислим периметр параллелограмма, используя известные данные.

Поскольку К и Р являются серединами ребра CD и ВС соответственно, то БК = КВ = (1/2)CD = (1/2)26 см = 13 см.

Аналогично, М и N являются серединами ребра AD и AC соответственно, поэтому АМ = МD = (1/2)AB = (1/2)30 см = 15 см.

Периметр параллелограмма равен сумме длин сторон. В нашем случае, стороны параллелограмма представлены отрезками АК, КР, РМ и МН.

Периметр = АК + КР + РМ + МН = 13 см + 13 см + 15 см + 15 см = 56 см.

Таким образом, периметр параллелограмма равен 56 см.