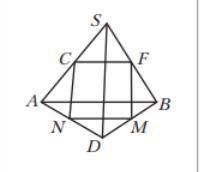
Точки F ,M,N,C- середины отрезков BS,DB,AD,AS соответственно. SD=30 см AB=36. Найти вид четырехугольника FMNC и его периметр . Рисунок ниже

вид треугольника пирамида в окружении

Пошаговое объяснение:

так написано в интарнете

Чтобы решить эту задачу, давайте сначала определим вид четырехугольника FMNC.

Так как точка F является серединой отрезка BS, а точка M является серединой отрезка DB, то отрезки FM и SN могут быть параллельны отрезку BD. Точно также, так как точка N является серединой отрезка AD, а точка C является серединой отрезка AS, то отрезки FN и MC могут быть параллельны отрезку AD. Теперь у нас есть параллельные отрезки FM и SN, а также параллельные отрезки FN и MC. Это значит, что угол MFC будет равен углу SNF, так как они соответственные углы.

Теперь рассмотрим треугольник FDS. У нас есть два равных участка FD и DS, так как точка F является серединой отрезка BS, и SD известно равным 30 см. Из этого следует, что угол FDS также будет равен углу SFD. Рассуждая аналогично, мы можем сказать, что угол ADS будет равен углу ASD.

Но угол ASD является прямым углом, так как это угол, лежащий на прямой AS, а угол NDC является прямым углом, так как это угол, лежащий на прямой ND. Итак, мы можем сделать вывод, что угол ASD равен углу NDC.

Теперь рассмотрим треугольник ASD. Поскольку мы знаем, что угол ASD равен углу NDC, а угол ADS равен углу ASD, то угол ADS также равен углу NDC. Это означает, что треугольники ASD и NDC являются подобными треугольниками, так как у них два угла, напротив равных сторон, равны между собой.

Теперь, зная, что угол MFC равен углу SNF, и что угол ADS равен углу NDC, мы можем сделать вывод, что четырехугольник FMNC является параллелограммом. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны.

Теперь можем найти периметр четырехугольника FMNC. Поскольку FMNC - параллелограмм, то противоположные стороны равны. Мы знаем, что AB = 36 см, поэтому FC также равна 36 см. Также мы знаем, что SD = 30 см, поэтому FN также равна 30 см. Значит, периметр четырехугольника FMNC равен 2 * (FC + FN) = 2 * (36 + 30) = 2 * 66 = 132 см.

Таким образом, вид четырехугольника FMNC - параллелограмм, а его периметр равен 132 см.