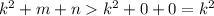Существуют ли такие натуральные числа m, n, k, что все три числа m^2+n+k, n^2+k+m, k^2+m+n являются квадратами натуральных чисел?
Другие вопросы по теме Математика
Популярные вопросы
- Напишите уравнение окружности с центром в точке с (−3; −2), если эта окружность...
2 - Сочнинение сказка на тему жила была крапива...
2 - Wy tavoriteani mal is a dog lt lives in the house lt has got kgs lt kan run...
1 - Синтетический разбор слова (вода ,выбивается ,утята,тявкнула,дворняжка.)...
2 - Велосипедное колесо вращается с частотой 6 об/с. под действием сил трения...
3 - Рассчитать относительную молекулярную массу для веществ: cuso4, mno, nh3...
1 - На складе есть красные коробки.в каждой красной коробке есть две синих.а...
2 - Нужно составить 3 односоставных предложения...
2 - Что относиться к органом переваривающие пищу...
1 - Отзыв о произведении рылеева смерть ярмака...
2
Пусть, не нарушая общности,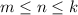
Тогда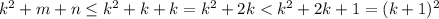
С другой стороны, т.к. числа натуральные,