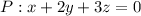Составить уравнение плоскости, проходящей через точку м0 (1; -2; 1) перпендикулярно прямой {x-2y+z-3=0 ; x+y-z+2=0} прямая = система уравнений
Другие вопросы по теме Математика
Популярные вопросы
- Записать логические выражения, которые имеют значение Истина только при...
2 - Прям угольный участок размером 48х60 покрывается плитками 6х 3. Можно ли...
2 - Одна сторона прямоугольника имеет длину 28 см, а другая - на 8 см. Расчеты...
3 - Найдите sin2a и cos2a если cosa (на фото)...
3 - написать выразительные средства Как один мужик двух генералов прокормил...
2 - Как можно охарактеризовать взаимоотношения Казахов с странами центрально-азиатскими...
3 - Стороны треугольника равны 8 см и 23 см. Найдите периметр квадрата...
2 - Узнайте некоторые элементы, которые даются формулы ...
2 - у рівнобедреному трикутнику основа дорівнює 10 см ,а кут при вершині 120...
3 - у нас СОЧ по русскому !??...
3
Плоскость имеет вид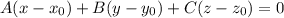 , где
, где 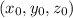 координаты точки, через которую проходит плоскость, а
координаты точки, через которую проходит плоскость, а 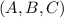 её нормальный вектор.
её нормальный вектор.
За нормальный вектор можно взять направляющий вектор прямой. Найдём его как векторное произведение нормальных векторов двух других плоскостей (через которые и задана прямая)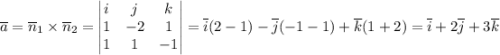
Итого наш ответ: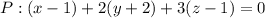
или