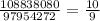Сократите дроби: 468/5616 1170/1404
34/255
150920/18480
2160/17820
8400/2184
268515/71604
108838080/97954272
Другие вопросы по теме Математика
Популярные вопросы
- Изотопы которых элементов образуются из радиоактивного изотопа 7/3 li после его...
2 - Решить. заранее ) сторона треугольника равна 14 см а две другие образуют угол...
3 - 10 предложений со словами чтобы, что бы; зато, за то; тоже, то же; также,так же....
3 - Закрытое акционерное общество «саунт» работает на рынке 5 лет. занимается поставкой...
2 - V(возд)=5м^3, ф=21%. найти v(в-ва)=?...
2 - Укажите вариант(ы) в котором (ых) представлено действительное причастие настоящего...
2 - Скільки існує натуральних двоцифрових чисел ab таких, що а8(восем это степень)...
2 - цитата із повчання дітям володимира мономаха . , я не смогла найти....
2 - Решите уравнение x^2-4/(x^2-3x+2)(x+3)=0...
2 - Умамы было три яблоко а у саши 4 сколько всего было яблок?...
1
Пример 1. Сократим дробь .
Решение. Наибольшее число, на которое делятся  и , равно . Поэтому чтобы сократить нашу дробь, поделим её числитель и знаменатель на :

Пример 2. Сократить на  дробь .
Решение. Делим числитель и знаменатель дроби на :

1)
2)
3)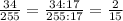
4)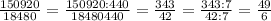
5)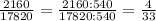
6)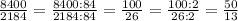
7) Этот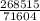 решу подробно.
решу подробно.
Выписываю одинаковые множители:
Теперь и числитель, и знаменатель делю на это число:
8)