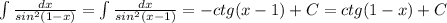Снеопределенными интегралами
Другие вопросы по теме Математика
Популярные вопросы
- Продолжите фразы об интересах человека современному человеку необходимо...
2 - Проверочные слова к словам: видел, степи, захотело,...
2 - Три лисы: алиса, лариса и инесса разговаривали на полянке. лариса:...
1 - Серебро объёмом 70 см3 имеет массу 735 г. 1)какова масса серебра объёмом...
1 - При каком значении переменной сумма 6х и 18х равна 72...
2 - Нужно провести наблюдение за тенью от предмета в условиях, зафиксировать...
2 - Узнать масса каждого мешка с мукой 5кг,10кг.3кг сколько будет решения...
3 - Запиши 5 послідовних чисел які передують найбільшому чотирьох значному...
1 - Придумай загадку, пословицу, шутку или считалку....
1 - Рассказ как я провел лето по языку 3 класс...
3
ответ: t¹² = 2x - 1
11. 1)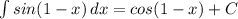
2)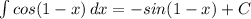
3)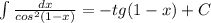
4)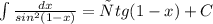
Пошаговое объяснение:
10. В неопределенном интеграле![\int\limits{\frac{\sqrt{2x-1} }{\sqrt[3]{2x-1} +\sqrt[4]{2x-1} } } \, dx](/tpl/images/0132/5542/a0680.png) следует применить подстановку
следует применить подстановку
1) t⁴ = 2x - 1; 2) t¹² = 2x - 1; 3) t³ = 2x - 1; 4) t² = 2x - 1;
Следует применять подстановку так, что бы полностью избавиться от знака радикала. Поскольку в знаменателе присутствует 3 и 4 степень то применяем подстановку 2) = 2x - 1; x = (t¹² +1)/2; dx = 6t¹¹
Теперь нужно сделать обратную подстановку![t=\sqrt[12]{2x-1}](/tpl/images/0132/5542/36e63.png)
11. Укажите соответствие между функциями и их неопределенными интегралами
1.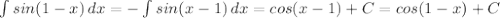
Проверка:(cos(1-x))' = -sin(1 - x)*(1 - x)' = sin(1 - x)
2.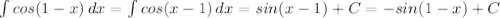
3.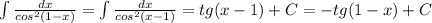
4.