1. Математика
  2. Сколько корней уравнения

Сколько корней уравнения sin4x=cos10^o(градусов) находятся в промежутке [0; pi]? (должно выйти 4)

ренат123456789 ренат123456789    1   16.08.2020 09:29    2

Ответы
Ka4erga3000 Ka4erga3000  15.10.2020 15:58

\sin4x=\cos10^\circ

Воспользуемся формулой приведения:

\sin4x=\sin(90^\circ- 10^\circ)

\sin4x=\sin80^\circ

\left[\begin{array}{l} 4x=80^\circ+360^\circ n\\ 4x=180^\circ-80^\circ+360^\circ n\end{array}

\left[\begin{array}{l} 4x=80^\circ+360^\circ n\\ 4x=100^\circ+360^\circ n\end{array}

\left[\begin{array}{l} x=20^\circ+90^\circ n\\ x=25^\circ+90^\circ n\end{array},\ n\in\mathbb{Z}

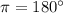Зная, что \pi=180^\circ выполним отбор корней.

Для первой серии:

0\leq 20^\circ+90^\circ n\leq 180^\circ

- 20^\circ\leq90^\circ n\leq 180^\circ- 20^\circ

- 20^\circ\leq90^\circ n\leq 160^\circ

- \dfrac{20}{90} \leq n\leq\dfrac{ 160}{ 90}

n=0:\ x_1=20^\circ+90^\circ\cdot0=\boxed{20^\circ}

n=1:\ x_2=20^\circ+90^\circ\cdot1=\boxed{110^\circ}

Для второй серии:

0\leq 25^\circ+90^\circ n\leq 180^\circ

- 25^\circ\leq90^\circ n\leq 180^\circ- 25^\circ

- 25^\circ\leq90^\circ n\leq 155^\circ

- \dfrac{25}{90} \leq n\leq\dfrac{ 155}{ 90}

n=0:\ x_3=25^\circ+90^\circ\cdot0=\boxed{25^\circ}

n=1:\ x_4=25^\circ+90^\circ\cdot1=\boxed{115^\circ}

ответ: 4 корня

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
какулькаТВ какулькаТВ  08.06.2019 21:40
Главный герой этой оперы-новгородский купец и путешесвенник,гусляр...
lerailina30040 lerailina30040  08.06.2019 21:40
Скорость поезда 72 км/ч.по параллельному его обгоняет поезд,движущийся со скоростью 84 км/ч.пассажир первого поезда заметил,что второй поезд шел мимо него 1мин 12сек.определите...
Karakulova2004 Karakulova2004  08.06.2019 21:40
Что я делаю в выходной сочинение на французском языке...
Boikamen Boikamen  08.06.2019 21:40
Как записать остаток после деления в столбик...
Dobro118 Dobro118  08.06.2019 21:40
Площадь прямоугольного треугольника 30корней из 3. один из углов 30 градусов. найти длину противолежащего этому углу катета....
Мозг66615 Мозг66615  08.06.2019 21:40
Арефмитический диктант 4 класс 2 часть...
Владислава3188125 Владислава3188125  08.06.2019 21:40
Известно, что a и b - положительные числа и a1/b 2)1/a 1/b 3)1/a=1/b 4)сравнить невозможно опишите кαк решилиω...
кот933 кот933  08.06.2019 21:40
Туристы проделали путь в 150 км, из них 48 км они шли пешком , а остальной путь плыли на плоту . сколько процентов от всего пути составляет путь на плоту?...
Pro100god322 Pro100god322  08.06.2019 21:40
Из 42 кг огурцов засолили 7 кг.какую часть огурцов засолили?...
gfyyfyftd gfyyfyftd  08.06.2019 21:40
1) 1-cos2a/1+cos2a + 1 2) 1-cos2a/1+tg^2(квадрат)a...

Популярные вопросы