Сколькими нулями оканчивается произведение всех чисел от единицы до ста?

Ответы

youlia86 04.10.2020 01:37

$1\cdot 2\cdot 3\cdot 4\cdot ...\cdot 100=100!$

Подсчитаем сколько раз приходится число 2 в факториал 100

$[\frac{100}{2}]+[\frac{100}{4}]+[\frac{100}{8}]+[\frac{100}{16}]+[\frac{100}{32}]+[\frac{100}{64}]=50+25+12+6+3+1=97$

В разложении на простые множители числа 100! двойка встречается ровно 97 раз.

Теперь подсчитаем сколько раз приходится число 5 в факториал 100

$[\frac{100}{5}]+[\frac{100}{25}]=20+4=24$

Число 5 встречается ровно 24 раза.

Значит,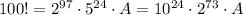 $100!=2^{97}\cdot 5^{24}\cdot A=10^{24}\cdot 2^{73}\cdot A$ , где А - некоторый множитель. И как видим, данное произведение оканчивается 24 нулями.

ответ: 24 нулями.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

анна2262 20.12.2020 20:50

Ов Применяя свойства сложения и умножения рациональных чисел, вычислите:рока-7-1,7+(-7)-(-3,7)=WВерных ответов: 3-7-(1,7+(-3,7)= -7:(-2)=14 -7-1,7+(-7)=- 7.1.7=...

AlexeyB96 20.12.2020 20:50

1. Найди значение выражения: a)2, 816, 8б) 12 4 31 8в)1, 21 23 3...

NastyaDND 20.12.2020 20:50

Найдите значение выражения: 14^-6*14^-12/14^-17...

ульянка37 20.12.2020 20:51

Выберите правильный ответ Какую часть займёт куб объёмом см от параллелепипеда объёмом 120м3Двадцатую...

VitaKoroleva851 20.12.2020 20:51

Вычеслите частное 1,034:0, 01...

tamirisis7sk 20.12.2020 20:51

Составьте два выражения для вычисления площади фигуры изображённой на рисунке.Докажите что полученный выражение тождественно равны. и сделаю лучшим ответом ...

VoinBogov 20.12.2020 20:51

На контроль поступило 20 стандартных и 18 бракованных деталей. Какова вероятность того, что вынутая наугад стандартная деталь?...

kitecat12 20.12.2020 20:51

Площадь прямоугольника 320 см2 а одна из сторон 200мм найди пириметр прямоугольника...

angelina2003po 20.12.2020 20:52

Вычислить периметр прямоугольника со сторонами 3 см 8 см...

kNoPoCHkA96 23.07.2019 00:20

Найдите сумму всех делителей числа 12 а)15; в)16; с)27; д)28...

Сколькими нулями оканчивается произведение всех чисел от единицы до ста?

Популярные вопросы