Сделайте все задание с полным решением
Другие вопросы по теме Математика
Популярные вопросы
- Сочинение по тринадцатый подвиг геракла...
2 - Имеется сплав серебра и меди массой 7 кг, содержащий 85% серебра....
1 - Докажите что значение выражения (4х+3)(х++5)(2х+4)+х(2х+3) не зависит...
3 - Eнаиболее заселённой частью океана является...
1 - Перевести на it doesn matter, pre-shool, elementary, to be a success,...
3 - 1килограмм мандаринов стоит 120 рублей. сколько маша заплатит за...
1 - Измерь стороны многоугольников в миллиметрах и найди периметр каждого...
2 - Два одинаковых заряда находятся на расстоянии 5 см друг от друга...
1 - Какие организмы синтезировать органические вещества из неорганических...
3 - Вкаких словах букв больше чем звуков мель, семья, море, ночь, якорь,...
1
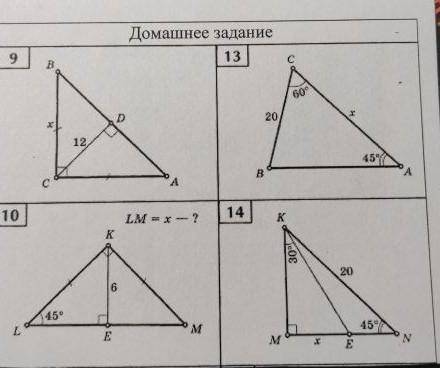
9.
CD - высота, но так как треугольник равноберенный, является также биссектрисой и медианой и по свойству она равна 1/2 биссектрисы.
= > АВ = 2 * 12 = 24.
Треугольник АВС - равнобедренный, значит
по т Пифагора:
10.
Найдем третий угол в треугольнике:
угол СВА = 180° - 60° - 45° = 75°
далее используем теорему синусов:
найдем sin(75°)
11.
из 9 задачи: LKM -равнобедренный => KE - высота, медиана, биссектриса.
LE = KE = 6.
12.
угол KNM = 45° => угол NKM = 45° => треугольник KNM - равнобедренный.