Розв’язати рівняння:
. У відповідь запишіть кількість коренів рівняння, які належать проміжку [-2π;2π]
Другие вопросы по теме Математика
Популярные вопросы
- Рожа,обожру,смотаться,пороюсь- это разговорные слова? (разговорные...
2 - 1)7ц-56кг 2)2т200кг+950кг 3)6м-4дм 4)5км105м-837м 5)10ц44кг: 36...
3 - Перевести на анг.яз.: белый каштан-символ киева. надо =)...
2 - Составить диалог на казахском языке на тему здоровье на 2их...
2 - Какие продукты - растительного или животного происхождения служат...
2 - Разложите на множители: 1) x^4-6x^2-27 2) x^4+x^2-20 x^4 значит...
2 - Разбор по составу слов: окрестные, проглядывали, распухшие, явственно,...
2 - Напишите, , сочинение на тему: how to become a scientist? (как...
1 - Стороны параллелограмма равны 4см и 5см, угол между ними 45 градусов....
1 - Сочинить стих на тему школьные годы 8...
3
Розглянемо проміжок![[-2\pi; \ 2\pi]](/tpl/images/1254/7495/f159a.png)
Скористаємося методом перебору коренів:
Якщо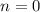 , то
, то 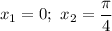
Якщо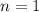 , то
, то 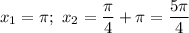
Якщо , то
, то ![x_{1} = 2\pi ; \ x_{2} = \dfrac{\pi }{4} + 2\pi = \dfrac{9\pi }{4} \notin [-2\pi ; \ 2\pi]](/tpl/images/1254/7495/05ad3.png)
Якщо , то
, то 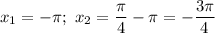
Якщо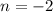 , то
, то 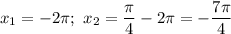
Отже, загальна кількість коренів, що входять у проміжок![[-2\pi; \ 2\pi]](/tpl/images/1254/7495/f159a.png) , дорівнює 9.
, дорівнює 9.
Відповідь: 9