Решите уравнение :
получите
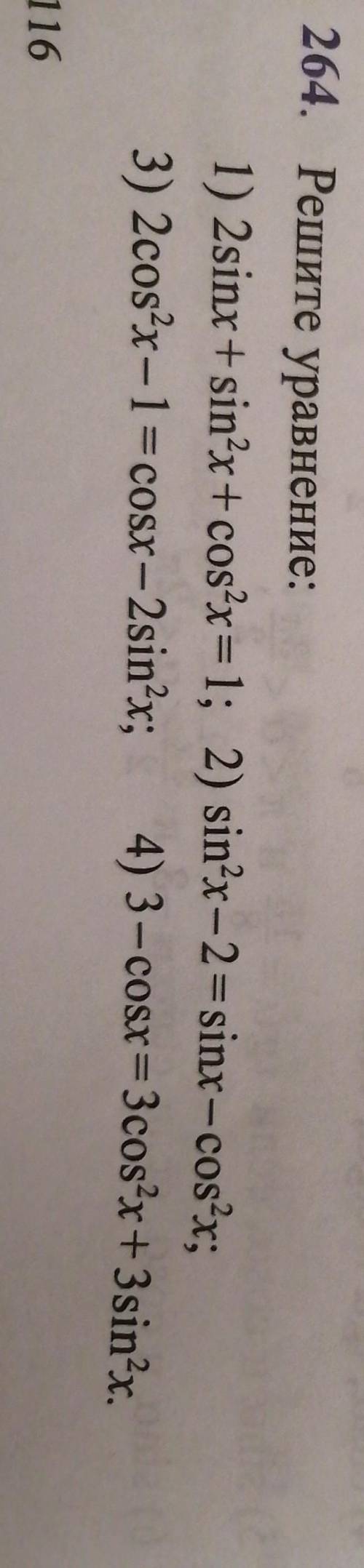
Другие вопросы по теме Математика
Популярные вопросы
- Нужно придумать слова учителю на последний звонок, типа слова . немного, буквально...
3 - Какой вид спорта не претерпел изменений со времен древнегреческих олимпийских...
2 - Написать программу на pascal. ввести 10 случайных чисел и посчитать количество...
1 - Нужно придумать интересный и веселый,(в тоже время и оригинальный)рецепт блюда(можно...
3 - Расскажите о строении водорослей. назовите их представителей. к какой группе...
2 - При равновесии рычага на его большее плечо, равное 30 см, действует сила 20...
3 - Обчисліть ккд важеля за якого вантаж з вагою 1000 ньютонів підняли на висоту...
3 - Традиционные общества в 19 веке кратко...
3 - Кто какие пословицы знает об улице?...
1 - Реши уравнение а÷186+216=313 (с+395)×219=434496...
2
sin²x + cos²x = 1
Исходя из этого:
1) 2sinx + sin²x + cos²x = 1
2sinx + 1 = 1
2sinx = 0
sinx = 0
x = arcsin0 = πn, (n€Z)
2) sin²x - 2 = sinx - cos²x
sin²x + cos²x - 2 = sinx
1 - 2 = sinx
sinx = -1
x = arcsin(-1) = 3π/2 ± 2πn, (n€Z)
3) 2cos²x - 1 = cosx - 2sin²x
2(sin²x + cos²x) - 1 = cosx
2•1 - 1 = cosx
cosx = 1
x = arccos1 = 2πn, (n€Z)
4) 3 - cosx = 3cos²x + 3sin²x
3 - cosx = 3(sin²x + cos²x)
3 - cosx = 3•1
cosx = 0
x = arccos0 = π/2 ± πn, (n€Z)