Решите уравнение 2sin^2x=1+cosx тригонометрия
Другие вопросы по теме Математика
Популярные вопросы
- При прямой перегонке нефть разделяют на три основные фракции:1)… 2)… 3)… Опишите...
3 - Знайти кількість нулів функції f(x)=sin3x....
1 - Виберіть якісна реакція на альдегіди а)біуретова реакція б)реакція срібного дзеркалав)ксантогенова...
3 - Комичное наименование мест, имена людей в рассказе Чехова Пересолил. !...
3 - УМОЛЯЮ Пользуясь законом сохранения массы, вычислите массу меди, образующейся...
2 - OD. Выпиши из предложений союзы,соединяющие однородные членыпредложения, определи...
3 - Твір на тему Уява Фантазія і Романтичність На основі твору Митькозавор с Васюківки...
2 - будь ласка до іть математика 6клас через 8хв здавати...
1 - я не понимаю ничего, это физика...
2 - за то что ответов в интернете нету, и если сочинение на страницу то поставлю...
3
Пошаговое объяснение:
Пусть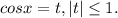 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
Значит