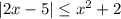 Решите модульное неравенство , если можно как можно подробней распишите
Решите модульное неравенство , если можно как можно подробней распишите
Другие вопросы по теме Математика
Популярные вопросы
- описание страны Танзия по плану 1. Какие карты надо использовать при описании...
2 - на подарки к Новому году было решено потратить 600 руб на шоколад 30%всей...
1 - Де тітонька Поллі шукає Тома...
2 - Музыка 7 класс Послушайте названные произведения, понаблюдайте за развитеем...
2 - Каз яз там все написано что сделать если что можете написать на русском я...
1 - ПушкинМихайловское: темы, мотивы и художественное своеобразие творчества....
3 - Напишіть невеликий твір: Уявіть себе учасником хрестового походу. Поділіться...
2 - Напишите план сцен в которых раскрывается характер Хлестакова (3 и 4 действие)...
1 - . В лесопунктах Карелии использовались трелевочные тракторы ТДТ-55. Лед выдерживает...
2 - English ibtidai sinif https://t.me/gunel2008Ребята у кого есть зайдите по...
3
(- ∞; -3 ] ∪ [1; + ∞ ).
Пошаговое объяснение:
1. Найдём нули подмодульного выражения:
2х - 5 = 0
2х = 5
х = 2,5
2.
а) Если х ≥ 2,5, то 2х - 5 ≥ 0, l2х - 5 l = 2х - 5 , тогда
l2х - 5 l ≤ х² + 2
2х - 5 ≤ х² + 2
х² + 2 - 2х + 5 ≥ 0
х² - 2х + 7 ≥ 0
(х-1)² + 6 ≥ 0 при всех х из рассматриваемого промежутка, т.е. х ∈ [2,5; + ∞ )
б) Если х < 2,5, то 2х - 5 < 0, l2х - 5 l = - 2х + 5 , тогда
l2х - 5 l ≤ х² + 2
- 2х + 5 ≤ х² + 2
х² + 2 + 2х - 5 ≥ 0
х² + 2х - 3 ≥ 0
(х - 1)(х + 3) ≥ 0
__+__[-3]__-__[1]__+__(2,5)...>
х ∈ (- ∞; -3 ] ∪ [1; 2,5)
Объединим решения, получим
х ∈ (- ∞; -3 ] ∪ [1; 2,5) ∪ [2,5; + ∞ )
х ∈ (- ∞; -3 ] ∪ [1; + ∞ ).
ответ: (- ∞; -3 ] ∪ [1; + ∞ ).