Решите МЕжконтрольная работа с пояснениями
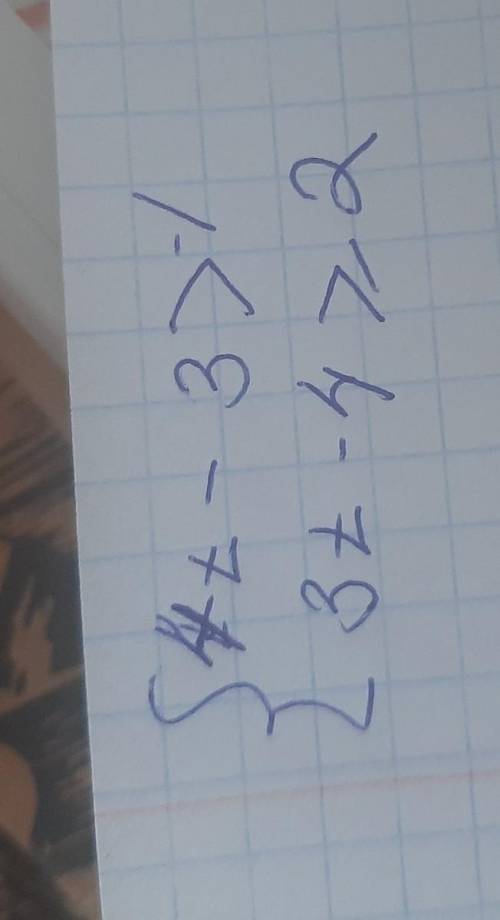
Другие вопросы по теме Математика
Популярные вопросы
- Впервом ящике 2 белых и 10 черных шаров, а во втором ящике 8 белых и 4 черных...
1 - Установите последовательность звеньев цепи питания: 1) рыба 2) растительный...
1 - Стороны оснований правильной треугольной усеченной пирамиды равны 6 см и...
1 - Особенности, которые отражают поведение человека как личности (выберите правильные...
2 - На сколько удалиться рыболовная леска жесткостью 1кн/м если ее растягивать...
1 - Какая формула позволяет определить число возможных стереоизомеров для оптических...
3 - Вдвойной системе счисления сумма 1010+1001...
2 - Составьте уравнения реакций лежащих в основе получения а) углекислого газа2)глюкозы...
3 - Стрех примеров проиллюстрируйте взаимовлияние народной, массовой и элитарной...
3 - Какая частица х испускается в результате следующей реакции: 1)альфа-частица2)электрон3)протон4)нейтрон...
3
ответ: x∈[2;+∞)
Пошаговое объяснение:
4t-3 > -1
3t-4 ≥ 2
Решаем каждое неравенство по отдельности
4t-3 > -1
4t > 2
t > 1/2
Отмечаем первое решение на отрезке методом интервалов:
°>x ° - выколотая точка
1/2
Записываем решение интервалом: x∈(1/2;+∞)
Решаем второе неравенство:
3t-4 ≥ 2
3t ≥ 6
t ≥ 2
Отмечаем второе решение на отрезке методом интервалов:
*>x * - не выколотая точка
2
Записываем решение интервалом: x∈[2;+∞)
Так как дана система неравенств,то соответственно найдём общее решение - объединим два решение в одно:
°*>x
1/2 2
Видим ,что оба решение пересекаются в полуинтервале x∈[2;+∞)
ответ: x∈[2;+∞)