решить задание по математике надо.

Исследовать на сходимость знакопеременный ряд.

ответ: ряд сходится

Пошаговое объяснение:чтобы исследовать знакочередующийся ряд на сходимость, надо применить признак Лейбница: если члены знакопеременного ряда убывают по модулю, то ряд сходится. (т.е. два условия, 1) ряд знакочеред-ся; 2) члены ряда монотонно убывают по модулю). Проверим эти условия:  1) Е (-1)ⁿ(3n-2/4n-3)²ⁿ = -1+4⁴/5⁴ - 7⁶/9⁶+ 10⁸/13⁸ -... = -1 + (4/5)⁴- (7/9)⁶  +(10/13)⁸ - (13/17)¹⁰+... ⇒ каждый следующий член ряда по модулю меньше предыдущего,   Неравенство |aₙ| < |aₙ₊₁|  здесь обосновать трудно, распишем несколько конкретных членов и всю цепочку: 1> (4/5)⁴ >(7/9)⁶> (10/13)⁸> (13/17)¹⁰>...> (3n-2/4n-3)²ⁿ  т.е. модуль общего члена ряда стремится к нулю: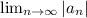 =  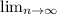 (3n-2/4n-3)²ⁿ =  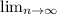(n(3 - 2/n / n(4 - 3/n) )²ⁿ = (3/4) ^∞ = 0. Значит ряд сходится.