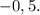Решить уравнение. Найти сумму корней уравнения, деленную на (пи)

1. Уравнение вида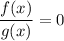 равносильно системе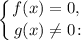

2. Решим уравнение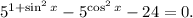

2.1. Поскольку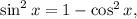 то

2.2. Используя свойство степеней имеем:

2.3. Сделаем замену: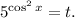 Тогда:

2.4. Преобразуем уравнение:

2.5. По теореме, обратной теореме Виета, имеем:

2.6. Делаем обратную замену:

2.7. Первое уравнение не имеет корней, поскольку правая часть не может быть отрицательной. Решим уравнение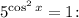

3. Определим ограничения: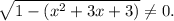

3.1. Ограничение для данного уравнения соответствует неравенству:

3.2. Раскроем скобки, приведем подобные слагаемые:

3.3. Умножим обе части неравенства на

3.4. Решением данного неравенства является промежуток

4. Отберем корни уравнения, принадлежащие промежутку

Пусть тогда

Пусть тогда

Пусть тогда

5. Решением данного уравнения является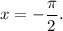

6. В ответ следует записать сумму корней (или корень, если он единственный), деленную на

ответ: