Решить систему дифференциальных уравнений: y'(t) = y(t) + z(t) z'(t) = t + y(t) + z(t)

Продифференцируем второе уравнение по переменной t, получим

Подставляем в первое уравнение:

Получили линейное неоднородное дифференциальное уравнение с постоянными коэффициентами со специальной правой частью:

Найдем сначала общее решение соответствующего однородного дифференциального уравнения:

Пусть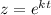 , получим характеристическое уравнение:

Общее решение однородного дифференциального уравнения

Рассмотрим полином правой части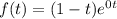 здесь 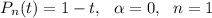. Сравнивая α с корнями характеристического уравнения и, принимая, во внимая что n = 0, частное решение будем искать в виде:

Подставляем в исходное диф. уравнение:

Приравниваем коэффициенты при степени t

Частное решение: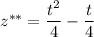

Общее решение линейного неоднородного дифференциального уравнения: