Решить неравенство методом рационализации ( метод знакотождественных множителей).

x ∈ (1/6; 1/3)∪(1/2; 2/3)

Пошаговое объяснение:

Область допустимых значений:

6·x-1>0, 2-3·x>0, ⇔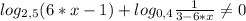

⇔ x>1/6, x<2/3, ⇔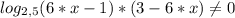

⇔ x∈(1/6; 2/3),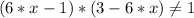 ⇔ x∈(1/6; 2/3), (3*x-1)²≠0 ⇔

⇔ x∈(1/6; 2/3), x≠1/3 ⇔ x∈(1/6; 1/3)∪(1/3; 2/3)

Применим метод  знакотождественных множителей:

В силу ОДЗ (3*x-1)²>0 и последнее неравенство равносильно неравенству:

(3*x-1)*(2*x-1)≥0 ⇔ x∈(-∞; 1/3]∪[1/2;+∞)

Тогда с учётом ОДЗ

x∈((1/6; 1/3)∪(1/3; 2/3))∩((-∞; 1/3]∪[1/2;+∞))=(1/6; 1/3)∪(1/2; 2/3)