Если ∠A, ∠B, ∠C и ∠D - внутренние углы выпуклого четырехугольника ABCD и ∠ C тупой, ∠A=125°, ∠B=100°, sin ∠C=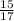 , то чему равен sin ∠D?
, то чему равен sin ∠D?
Другие вопросы по теме Геометрия
Популярные вопросы
- Рівняння руху тіла ,що рухається рівноприскоренно зі стану спокою...
1 - Казак тили 3 сынып 32 бет 55 жаттыгу...
2 - Внимательно прочитай текст из энциклопедии для детей.языкознание....
2 - Почему вечно удаляет вопросы, которые я пишу или ответы которые мне...
2 - Записать по 3 примера на каждый из 5 признаков делимости....
1 - Вопрос на правильность дефиса в предложении. на такой курорт слетелись...
1 - Знайти найбільш і найменш значення. y=-2x-1 [ -2; 4]...
1 - Короткострокові і довгострокові наслідки, коли люди не дбають про...
2 - Гурилдей шубыра сулар тасыса,тениз болмас магынасы...
2 - Укажите названия карт атласа с наименьшими искажениями территории...
1
Объяснение:
<А=125 градусов
<В=100 градусов
sin<C=15/17=0,88235
<C=118 градусов
<D=360-(<A+<B+<C)=
=360-(125+100+118)=17 градусов
sin<D=sin17=0,292372
D =360-A-B-C =360-125-100-C =135-C
sinD =sin(135-C) =sin135 cosC - cos135 sinC
sin135 =√2/2
cos135 = -√2/2
cosC = -√(1-sinC^2) = -8/17 (C>90)
sinD = √2/2 *(-8/17) - (-√2/2) *15/17 = 7√2/34